2.1 Analysis of time series  (Page 4/6)

Another approach available to us is to think of a data as a weighted average of some error terms that are assumed to have a mean of zero, have a fixed variance, and be uncorrelated over time That is, we assume ${\epsilon }_t~\left(0,{\sigma }^2\right)$ , where the distribution is not specified, and $E\left({\epsilon }_i{\epsilon }_j\right)=0$ for all $i\ne j$ . :

A data series exhibiting this pattern is called a moving average process or MA(q). The error tern is known in the literature as white noise. A data series that has both autoregressive and moving average characteristics is call an autoregressive moving average (ARMA) series; an ARMA(p, q) is:

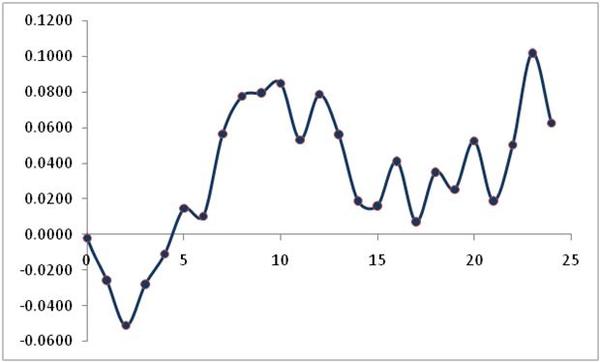
It may help to show two series constructed to have different ARMA patterns. Figure 7 shows one of the potential time series generated by the ARMA(2,1) process:

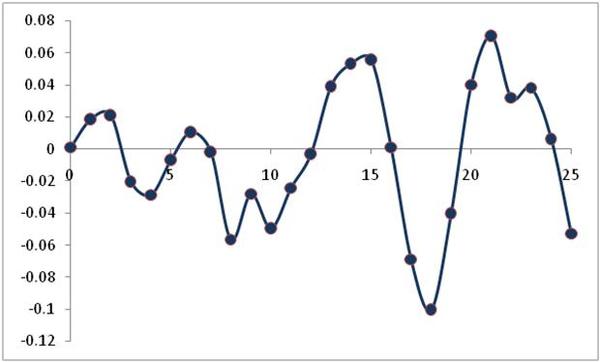
Figure 8 shows one potential time series generated by the ARMA(1,1) process:

Stationarity

Consider the time-series $y_t.$ We define this stochastic process as covariance stationary if

The last term, ${\gamma }_s,$ is known as the autocovariance. A time-series is defined to be covariance stationary if its mean and all its autocovariances are unaffected by a change of time origin. We define the autocorrelation between $y_t$ and $y_{t-s}$ as:

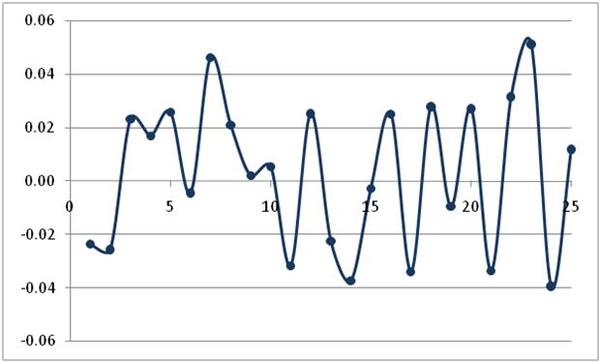
Quite often you can create a stationary time-series from a non-stationary time-series by taking the first-differences of the non-stationary series. If the first difference does not produce a stationary series, then one continues to take first differences until you find a stationary series. For instance, the time-series shown in Figure 7 appears to be non-stationary. The first differences of this series is shown in Figure 9. Using the imperfect eye, it would appear that the first differences of (13) is stationary. However, we really cannot tell anything for sure from the graph of a data set. We need to use the restrictions of the parameters derived in advanced texts to determine if a data set is stationary. These methods make use of the mathematics of difference equations. See advanced texts like Enders (1995: pp. 68-77) for examples of the derivation of the conditions necessary for an ARMA( p , q ) time-series to be stationary.

The autocorrelation function

One of the major ways to identify the structure of a time series is to look at the autocorrelation function. The autocorrelation function, ${\rho }_s,$ is the correlation between $y_t$ and $y_{t-s}.$ Stata uses the following formula to estimate it [StataCorp: p. 60] for a time-series:

The researcher then has to compare the actual autocorrelation function with the theoretical autocorrelation for comparable data series. To see to use the autocorrelation function consider the following five time series AR(1) is the same as ARMA(1, 0) :