| << Chapter < Page | Chapter >> Page > |
In this section, we consider the problem of finding the tangent plane to a surface, which is analogous to finding the equation of a tangent line to a curve when the curve is defined by the graph of a function of one variable, The slope of the tangent line at the point is given by what is the slope of a tangent plane? We learned about the equation of a plane in Equations of Lines and Planes in Space ; in this section, we see how it can be applied to the problem at hand.
Intuitively, it seems clear that, in a plane, only one line can be tangent to a curve at a point. However, in three-dimensional space, many lines can be tangent to a given point. If these lines lie in the same plane, they determine the tangent plane at that point. A more intuitive way to think of a tangent plane is to assume the surface is smooth at that point (no corners). Then, a tangent line to the surface at that point in any direction does not have any abrupt changes in slope because the direction changes smoothly. Therefore, in a small-enough neighborhood around the point, a tangent plane touches the surface at that point only.
Let be a point on a surface and let be any curve passing through and lying entirely in If the tangent lines to all such curves at lie in the same plane, then this plane is called the tangent plane to at ( [link] ).
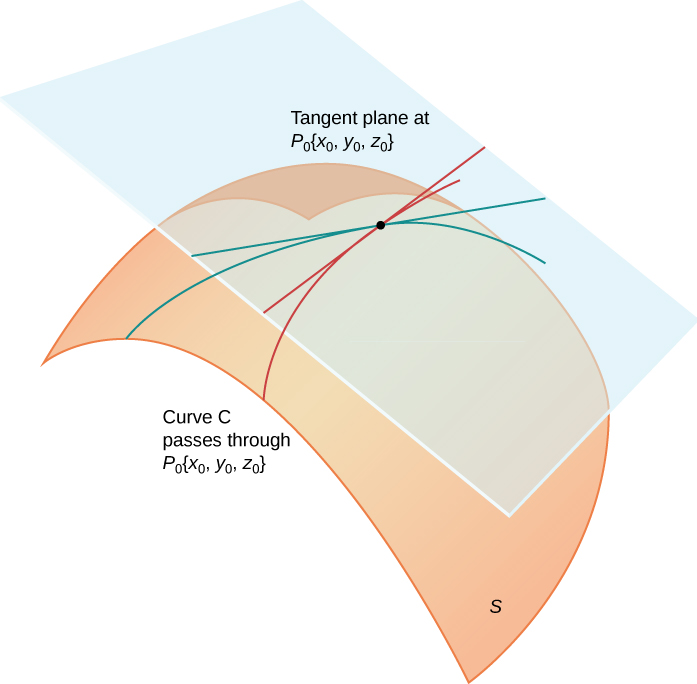
For a tangent plane to a surface to exist at a point on that surface, it is sufficient for the function that defines the surface to be differentiable at that point. We define the term tangent plane here and then explore the idea intuitively.
Let be a surface defined by a differentiable function and let be a point in the domain of Then, the equation of the tangent plane to at is given by
To see why this formula is correct, let’s first find two tangent lines to the surface The equation of the tangent line to the curve that is represented by the intersection of with the vertical trace given by is Similarly, the equation of the tangent line to the curve that is represented by the intersection of with the vertical trace given by is A parallel vector to the first tangent line is a parallel vector to the second tangent line is We can take the cross product of these two vectors:
This vector is perpendicular to both lines and is therefore perpendicular to the tangent plane. We can use this vector as a normal vector to the tangent plane, along with the point in the equation for a plane:

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?