2.2 Least squared error design of fir filters  (Page 6/13)

and illustrated in [link] For N odd, the ideal infinitely and shifted filter coefficients are the inverse DTFT of this amplitude given by

with the indeterminate ${\widehat{h}}_d\left(0\right)=\frac{{\omega }_0^2}{2{\pi }^2}$ . This is now truncated and shifted by $M=(N-1)/2$ to give the optimal, causal length- $N$ FIR filter coefficients as

and $h\left(n\right)=0$ otherwise. The corresponding derivation for an even length starts with the inverseDTFT for a shifted even length filter in Equation 15 from Chebyshev or Equal Ripple Error Approximation Filters and after shifting by $N/2$ gives the same result as [link] .

Ideal differentiator plus lowpass filter

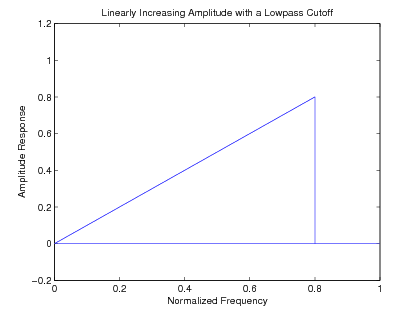
Fortunately the inverse DTFT for an ideal differentiator combined with a lowpass filter can also be analytically evaluated. The ideal amplituderesponse is the same as [link] and [link] but, since this case has an odd symmetric impulse response, the inverse DTFT uses sine functions which forodd $N$ gives

with the indeterminate ${\widehat{h}}_d\left(0\right)=0$ . This is now truncated and shifted by $M=(N-1)/2$ to give the optimal, causal length- $N$ FIR filter coefficients as

and $h\left(n\right)=0$ otherwise. Again the corresponding derivation for an even length gives the sameresult as in [link] . Note this very general single formula includes as special cases the odd and even length full band ( ${\omega }_0=\pi$ ) differentiator given in [link] . Also note that for a full band differentiator, an even length is much preferred because of the zero at $\omega =\pi$ for an odd length. However, for the differentiator with a lowpass filter, the zero aids in the lowpass filtering and, therefore,might be an advantage.

Hilbert transformer

The inverse DTFT for an ideal Hilbert transform [link] combined with a lowpass filter can also be analytically evaluated. The ideal amplituderesponse is the same as [link] but with a constant phase shift of $\varphi =\pi /2$ . Since this case has an odd symmetric impulse response, the inverse DTFT uses sine functions which for odd $N$ which gives

with the indeterminate ${\widehat{h}}_d\left(0\right)=0$ . This is now truncated and shifted by $M=(N-1)/2$ to give the optimal, causal length- $N$ FIR filter coefficients as

and $h\left(n\right)=0$ otherwise. Again the corresponding derivation for an even length gives the same result as in [link] . The ideal amplitude response is shown in [link] .

Spline transition band design

All of the four lowpass filters described above exhibit the Gibbs phenomenon when truncated to a finite length. To remove this effect andto give a more explicit specification of the pass and stopband edges, a transition band is inserted between the pass and stopband. A transitionfunction can be placed in this band to make the total desired amplitude response a continuous function.

If we use a $p^{th}$ order spline as the transition function, the effect of adding this transition band to the basic lowpass filter ideal amplitudegiven in [link] is to multiply the ideal impulse response in [link] by a the $P^{th}$ power of a sinc function to give