| << Chapter < Page | Chapter >> Page > |
The quotient of and is
The quotient of and twelve is
Three-fourths of is
Seven-tenths of is
divided by equals negative
Three-fourths of is the same as
The sum of five-sixths and is
The difference of and one-fourth is
Shopping Teresa bought a pair of shoes on sale for The sale price was of the regular price. Find the regular price of the shoes by solving the equation
Playhouse The table in a child’s playhouse is of an adult-size table. The playhouse table is inches high. Find the height of an adult-size table by solving the equation
30 inches
[link] describes three methods to solve the equation Which method do you prefer? Why?
Richard thinks the solution to the equation is Explain why Richard is wrong.
Answers will vary.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
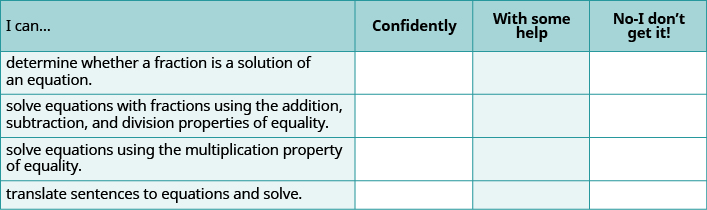
ⓑ Overall, after looking at the checklist, do you think you are well-prepared for the next Chapter? Why or why not?
In the following exercises, name the fraction of each figure that is shaded.
In the following exercises, name the improper fractions. Then write each improper fraction as a mixed number.
In the following exercises, convert the improper fraction to a mixed number.
In the following exercises, convert the mixed number to an improper fraction.
Find three fractions equivalent to Show your work, using figures or algebra.
Find three fractions equivalent to Show your work, using figures or algebra.
Answers may vary.
In the following exercises, locate the numbers on a number line.
In the following exercises, order each pair of numbers, using or
In the following exercises, simplify.
In the following exercises, multiply.
In the following exercises, find the reciprocal.
Fill in the chart.
| Opposite | Absolute Value | Reciprocal | |
|---|---|---|---|
In the following exercises, divide.
In the following exercises, perform the indicated operation.
In the following exercises, translate the English phrase into an algebraic expression.
the quotient of and
In the following exercises, simplify the complex fraction
In the following exercises, simplify.
In the following exercises, add.
In the following exercises, subtract.
In the following exercises, find the least common denominator.
In the following exercises, change to equivalent fractions using the given LCD.
In the following exercises, perform the indicated operations and simplify.
In the following exercises, evaluate.
In the following exercises, perform the indicated operation.
In the following exercises, determine whether the each number is a solution of the given equation.
In the following exercises, solve the equation.
In the following exercises, translate and solve.
The sum of two-thirds and is
The quotient of and is
Convert the improper fraction to a mixed number.
Convert the mixed number to an improper fraction.
Locate the numbers on a number line.
In the following exercises, simplify.
Evaluate.
In the following exercises, solve the equation.
Translate and solve: The quotient of and is Solve for

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?