| << Chapter < Page | Chapter >> Page > |
Notice the difference in the two previous examples:
The first step in simplifying an expression using the Quotient Property for Exponents is to determine whether the exponent is larger in the numerator or the denominator.
Simplify: ⓐ ⓑ
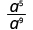 | |
| Use the Quotient Property, . |
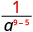 |
| Simplify. |
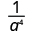 |
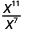 | |
| Use the Quotient Property, . |
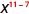 |
| Simplify. |
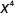 |
A special case of the Quotient Property is when the exponents of the numerator and denominator are equal, such as an expression like . From your earlier work with fractions, you know that:
In words, a number divided by itself is 1. So, , for any , since any number divided by itself is 1.
The Quotient Property for Exponents shows us how to simplify when and when by subtracting exponents. What if ?
Consider , which we know is 1.
Now we will simplify in two ways to lead us to the definition of the zero exponent. In general, for :
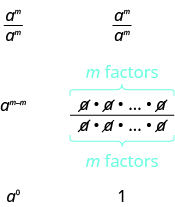
We see simplifies to and to 1. So .
If is a non-zero number, then .
Any nonzero number raised to the zero power is 1.
In this text, we assume any variable that we raise to the zero power is not zero.
Simplify: ⓐ ⓑ
The definition says any non-zero number raised to the zero power is 1.
Now that we have defined the zero exponent, we can expand all the Properties of Exponents to include whole number exponents.
What about raising an expression to the zero power? Let’s look at . We can use the product to a power rule to rewrite this expression.
This tells us that any nonzero expression raised to the zero power is one.
Now we will look at an example that will lead us to the Quotient to a Power Property.
Notice that the exponent applies to both the numerator and the denominator.
We see that is .

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?