| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
Remember that an exponent indicates repeated multiplication of the same quantity. For example, means to multiply four factors of so means This format is known as exponential notation .
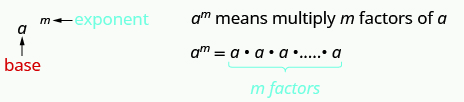
This is read to the power.
In the expression the exponent tells us how many times we use the base as a factor.

Before we begin working with variable expressions containing exponents, let’s simplify a few expressions involving only numbers.
Simplify:
| ⓐ | |
| Multiply 3 factors of 5. | |
| Simplify. |
| ⓑ | |
| Multiply 1 factor of 9. |
Simplify:
| ⓐ | |
| Multiply two factors. | |
| Simplify. |
| ⓑ | |
| Multiply two factors. | |
| Simplify. |
Simplify:
| ⓐ | |
| Multiply four factors of −3. | |
| Simplify. |
| ⓑ | |
| Multiply two factors. | |
| Simplify. |
Notice the similarities and differences in parts ⓐ and ⓑ . Why are the answers different? In part ⓐ the parentheses tell us to raise the (−3) to the 4 th power. In part ⓑ we raise only the 3 to the 4 th power and then find the opposite.
You have seen that when you combine like terms by adding and subtracting, you need to have the same base with the same exponent. But when you multiply and divide, the exponents may be different, and sometimes the bases may be different, too. We’ll derive the properties of exponents by looking for patterns in several examples. All the exponent properties hold true for any real numbers, but right now we will only use whole number exponents.
First, we will look at an example that leads to the Product Property.
|
| |
| What does this mean?
How many factors altogether? |
 |
| So, we have |
|
| Notice that 5 is the sum of the exponents, 2 and 3. |
|
The base stayed the same and we added the exponents. This leads to the Product Property for Exponents.
If is a real number and are counting numbers, then
To multiply with like bases, add the exponents.
An example with numbers helps to verify this property.
Simplify:
| Rewrite, | |
| Use the product property, |
|
| Simplify. |

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?