| << Chapter < Page | Chapter >> Page > |
Recall that a context tree source is similar to a Markov source, where the number of states is greatly reduced. Let be the set of leaves of a context tree source, then the redundancy is
where is the number of leaves, and we have instead of , because each state generated symbols, on average. In contrast, the redundancy for a Markov representation of the tree source is much larger. Therefore, tree sources are greatly preferable in practice, they offer a significant reductionin redundancy.
How can we compress universally over the parametric class of tree sources? Suppose that we knew , that is we knew the set of leaves. Then we could process sequentially, where for each we can determine what state its context is in, that is the unique suffix of that belongs to the set of leaf labels in . Having determined that we are in some state , can be computed by examining all previous times that we were in state and computing the probability with the Krichevsky-Trofimov approach based on the number of times that the following symbol(after ) was 0 or 1. In fact, we can store symbol counts and for all , update them sequentially as we process , and compute efficiently. (The actual translation to bits is performed with an arithmetic encoder.)
While promising, this approach above requires to know . How do we compute the optimal from the data?
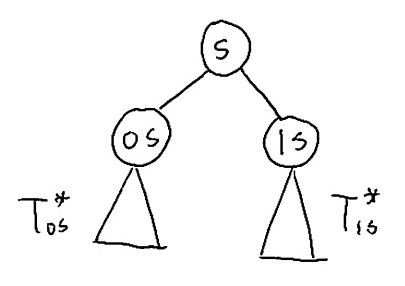
Semi-predictive coding : The semi-predictive approach to encoding for context tree sources [link] is to scan the data twice, where in the first scan we estimate and in the second scan we encode from , as described above. Let us describe a procedure for computing the optimal among tree sources whose depth is bounded by . This procedure is visualized in [link] . As suggested above, we count , the number of times that each possible symbol appeared in context , for all . Having computed all the symbol counts, we process the depth- tree in a bottom-top fashion, from the leaves to the root, where for each internal node of the tree (that is, where ), we track , the optimal tree structure rooted at to encode symbols whose context ends with , and the minimum description lengths (MDL) required for encoding these symbols.
Without loss of generality, consider the simple case of a binary alphabet . When processing we have already computed the symbol counts and , , , the optimal trees and , and the minimum description lengths (MDL) and . We have two options for state .

Notification Switch
Would you like to follow the 'Universal algorithms in signal processing and communications' conversation and receive update notifications?