| << Chapter < Page | Chapter >> Page > |
Graph the equation
The equation has only variable, The value of is constant. All the ordered pairs in the table have the same -coordinate, . We choose and as values for
The graph is a horizontal line passing through the -axis at as shown.
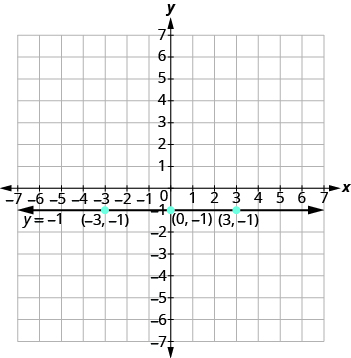
The equations for vertical and horizontal lines look very similar to equations like What is the difference between the equations and
The equation has both and The value of depends on the value of The changes according to the value of
The equation has only one variable. The value of is constant. The is always It does not depend on the value of
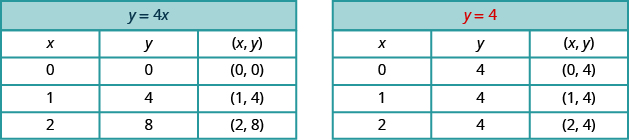
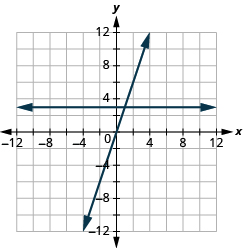
The graph shows both equations.
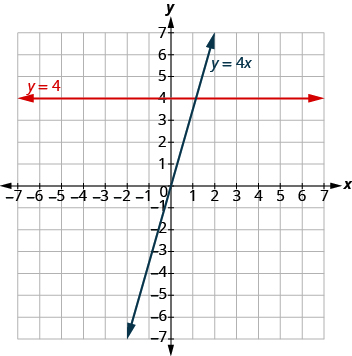
Notice that the equation gives a slanted line whereas gives a horizontal line.
Graph and in the same rectangular coordinate system.
Find three solutions for each equation. Notice that the first equation has the variable
while the second does not. Solutions for both equations are listed.

The graph shows both equations.

Graph the equations in the same rectangular coordinate system: and
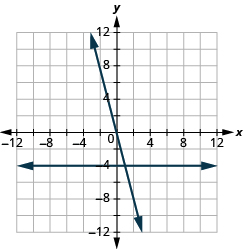
Graph the equations in the same rectangular coordinate system: and
Recognize the Relation Between the Solutions of an Equation and its Graph
For each ordered pair, decide
Graph a Linear Equation by Plotting Points
In the following exercises, graph by plotting points.
Graph Vertical and Horizontal lines
In the following exercises, graph the vertical and horizontal lines.
In the following exercises, graph each pair of equations in the same rectangular coordinate system.
Mixed Practice
In the following exercises, graph each equation.
Motor home cost The Robinsons rented a motor home for one week to go on vacation. It cost them plus per mile to rent the motor home, so the linear equation gives the cost, for driving miles. Calculate the rental cost for driving miles, and then graph the line.
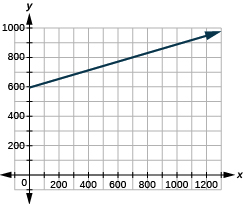
$722, $850, $978
Weekly earning At the art gallery where he works, Salvador gets paid per week plus of the sales he makes, so the equation gives the amount he earns for selling dollars of artwork. Calculate the amount Salvador earns for selling and then graph the line.
Explain how you would choose three to make a table to graph the line
Answers will vary.
What is the difference between the equations of a vertical and a horizontal line?
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

ⓑ After reviewing this checklist, what will you do to become confident for all objectives?

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?