| << Chapter < Page | Chapter >> Page > |
When solving an inequality, explain what happened from Step 1 to Step 2:
When we divide both sides by a negative it changes the sign of both sides so the sense of the inequality sign changes.
When solving an inequality, we arrive at:
Explain what our solution set is.
When writing our solution in interval notation, how do we represent all the real numbers?
When solving an inequality, we arrive at:
Explain what our solution set is.
Describe how to graph
We start by finding the x -intercept, or where the function = 0. Once we have that point, which is we graph to the right the straight line graph and then when we draw it to the left we plot positive y values, taking the absolute value of them.
For the following exercises, solve the inequality. Write your final answer in interval notation.
For the following exercises, solve the inequality involving absolute value. Write your final answer in interval notation.
For the following exercises, describe all the x -values within or including a distance of the given values.
Distance of 5 units from the number 7
Distance of10 units from the number 4
For the following exercises, solve the compound inequality. Express your answer using inequality signs, and then write your answer using interval notation.
For the following exercises, graph the function. Observe the points of intersection and shade the x -axis representing the solution set to the inequality. Show your graph and write your final answer in interval notation.
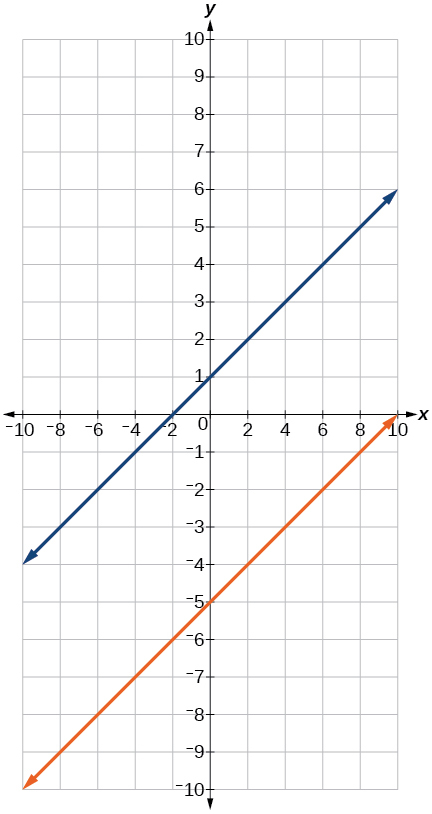
For the following exercises, graph both straight lines (left-hand side being y1 and right-hand side being y2) on the same axes. Find the point of intersection and solve the inequality by observing where it is true comparing the y -values of the lines.
Where the blue line is above the orange line; point of intersection is
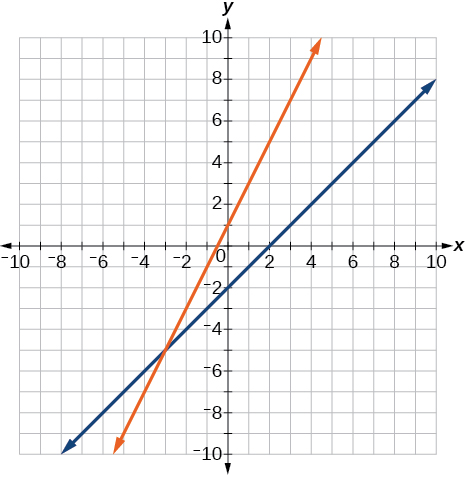
Where the blue line is above the orange line; always. All real numbers.
For the following exercises, write the set in interval notation.
For the following exercises, write the interval in set-builder notation.
For the following exercises, write the set of numbers represented on the number line in interval notation.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?