| << Chapter < Page | Chapter >> Page > |
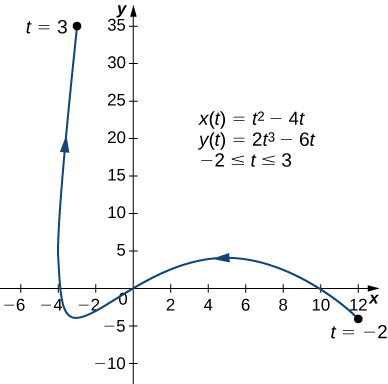
Calculate the derivative for the plane curve defined by the equations
and locate any critical points on its graph.
and
so
This expression is undefined when
and equal to zero when
Find the equation of the tangent line to the curve defined by the equations
First find the slope of the tangent line using [link] , which means calculating and
Next substitute these into the equation:
When so this is the slope of the tangent line. Calculating and gives
which corresponds to the point on the graph ( [link] ). Now use the point-slope form of the equation of a line to find the equation of the tangent line:
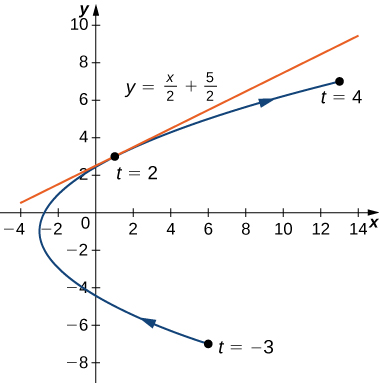
Find the equation of the tangent line to the curve defined by the equations
The equation of the tangent line is
Our next goal is to see how to take the second derivative of a function defined parametrically. The second derivative of a function is defined to be the derivative of the first derivative; that is,
Since we can replace the on both sides of this equation with This gives us
If we know as a function of t, then this formula is straightforward to apply.
Calculate the second derivative for the plane curve defined by the parametric equations
Calculate the second derivative for the plane curve defined by the equations
and locate any critical points on its graph.
Critical points
Now that we have seen how to calculate the derivative of a plane curve, the next question is this: How do we find the area under a curve defined parametrically? Recall the cycloid defined by the equations Suppose we want to find the area of the shaded region in the following graph.
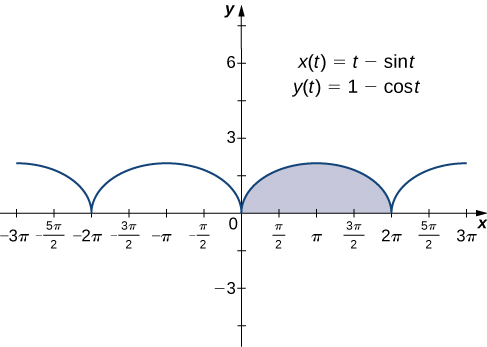
To derive a formula for the area under the curve defined by the functions
we assume that is differentiable and start with an equal partition of the interval Suppose and consider the following graph.
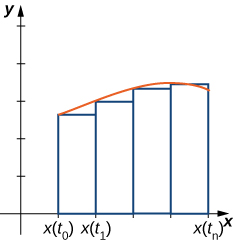
We use rectangles to approximate the area under the curve. The height of a typical rectangle in this parametrization is for some value in the i th subinterval, and the width can be calculated as Thus the area of the i th rectangle is given by

Notification Switch
Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?