| << Chapter < Page | Chapter >> Page > |
Perform this subtraction.
The number 503 contains a single zero
The number to the immediate left of 0 is 5. Decrease 5 by 1.

Borrow from the 10 and proceed.

Perform each subtraction.
Consider the problem
In this case, we have a group of zeros.
![]()
Since we cannot borrow any tens or hundreds, we must borrow 1 thousand. One thousand = 10 hundreds.
![]()
We can now borrow 1 hundred from 10 hundreds. One hundred = 10 tens.

We can now borrow 1 ten from 10 tens. One ten = 10 ones.
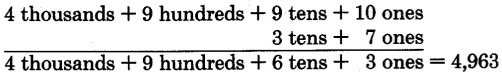
From observations made in this procedure we can suggest the following method for borrowing from a group of zeros.
Perform each subtraction.
The number 40,000 contains a group of zeros.
The number to the immediate left of the group is 4. Decrease 4 by 1.
Make each 0, except the rightmost one, 9. Make the rightmost 0 a 10.

Subtract as usual.
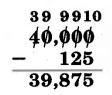
The number 8,000,006 contains a group of zeros.
Make each zero, except the rightmost one, 9. Make the rightmost 0 a 10.

To perform the subtraction, we’ll need to borrow from the ten.

Perform each subtraction.
In practice, calculators are used to find the difference between two whole numbers.
Find the difference between 1006 and 284.
| Display Reads | ||
| Type | 1006 | 1006 |
| Press | 1006 | |
| Type | 284 | 284 |
| Press | = | 722 |
The difference between 1006 and 284 is 722.
(What happens if you type 284 first and then 1006? We'll study such numbers in [link] Chapter 10.)
Use a calculator to find the difference between 7338 and 2809.
4,529
Use a calculator to find the difference between 31,060,001 and 8,591,774.
22,468,227
For the following problems, perform the subtractions. You may check each difference with a calculator.
For the following problems, perform each subtraction.
Subtract 63 from 92.

Notification Switch
Would you like to follow the 'Fundamentals of mathematics' conversation and receive update notifications?