| << Chapter < Page | Chapter >> Page > |
Perform the following divisions.
The process of division also works when the divisor consists of two or more digits. We now make educated guesses using the first digit of the divisor and one or two digits of the dividend.
Find .
Use the first digit of the divisor and the first two digits of the dividend to make the educated guess.
3 goes into 22 at most 7 times.
Try 7: which is greater than 223. Reduce the estimate.
Try 6: which is less than 223.
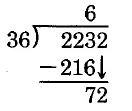
Divide 3 into 7 to estimate the number of times 36 goes into 72. The 3 goes into 7 at most 2 times.
Try 2: .
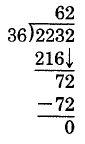
Check :
![]()
Thus, .
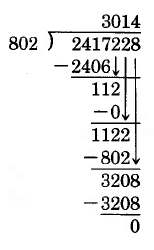
Find .
First, the educated guess: . Then , which is less than 2417. Use 3 as the guess. Since , and 2406 has four digits, place the 3 above the fourth digit of the dividend.
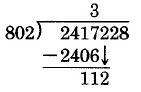
Subtract: 2417 - 2406 = 11.
Bring down the 2.
The divisor 802 goes into 112 at most 0 times. Use 0.

The 8 goes into 11 at most 1 time, and , which is less than 1122. Try 1.
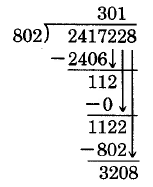
Subtract
Bring down the 8.
8 goes into 32 at most 4 times.
.
Use 4.
Check:
![]()
Thus, .
Perform the following divisions.
We might wonder how many times 4 is contained in 10. Repeated subtraction yields
Since the remainder is less than 4, we stop the subtraction. Thus, 4 goes into 10 two times with 2 remaining. We can write this as a division as follows.
Since 4 does not divide into 2 (the remainder is less than the divisor) and there are no digits to bring down to continue the process, we are done. We write
or
Find .
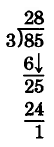
There are no more digits to bring down to continue the process. We are done. One is the remainder.
Check: Multiply 28 and 3, then add 1.
Thus, .
Perform the following divisions.
The calculator can be useful for finding quotients with single and multiple digit divisors. If, however, the division should result in a remainder, the calculator is unable to provide us with the particular value of the remainder. Also, some calculators (most nonscientific) are unable to perform divisions in which one of the numbers has more than eight digits.

Notification Switch
Would you like to follow the 'Fundamentals of mathematics' conversation and receive update notifications?