| << Chapter < Page | Chapter >> Page > |
Find the interval and radius of convergence for the series
The interval of convergence is The radius of convergence is
Being able to represent a function by an “infinite polynomial” is a powerful tool. Polynomial functions are the easiest functions to analyze, since they only involve the basic arithmetic operations of addition, subtraction, multiplication, and division. If we can represent a complicated function by an infinite polynomial, we can use the polynomial representation to differentiate or integrate it. In addition, we can use a truncated version of the polynomial expression to approximate values of the function. So, the question is, when can we represent a function by a power series?
Consider again the geometric series
Recall that the geometric series
converges if and only if In that case, it converges to Therefore, if the series in [link] converges to and we write
As a result, we are able to represent the function by the power series
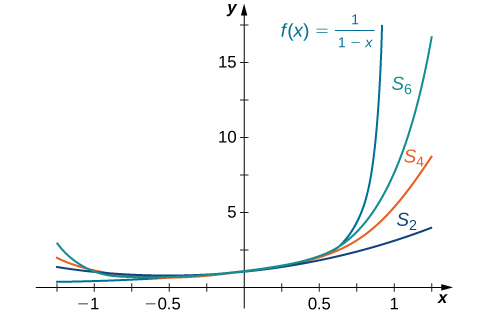
We now show graphically how this series provides a representation for the function by comparing the graph of f with the graphs of several of the partial sums of this infinite series.
Sketch a graph of and the graphs of the corresponding partial sums for on the interval Comment on the approximation as N increases.
From the graph in [link] you see that as N increases, becomes a better approximation for for x in the interval
Sketch a graph of and the corresponding partial sums for on the interval
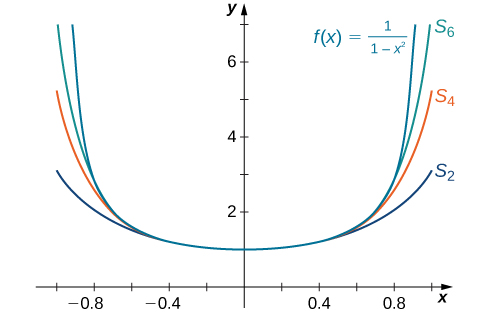
Next we consider functions involving an expression similar to the sum of a geometric series and show how to represent these functions using power series.
Use a power series to represent each of the following functions Find the interval of convergence.

Notification Switch
Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?