| << Chapter < Page | Chapter >> Page > |
This module describes the type of signals acted on by the Discrete Time Fourier Transform.
The Discrete Time Fourier Transform maps arbitrary discrete time signals in to finite-length, discrete-frequency signals in .

When a function repeats itself exactly after some given period, or cycle, we say it's periodic . A periodic function can be mathematically defined as:
We can think of periodic functions (with period ) two different ways:
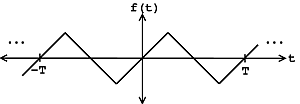

An
aperiodic DT function, however,
does not repeat for
any
;
Suppose we have such an aperiodic function . We can construct a periodic extension of called , where is repeated every seconds. If we take the limit as , we obtain a precise model of an aperiodic signal for which all rules that govern periodic signals can be applied, including Fourier Analysis (with an important modification). For more detail on this distinction, see the module on the Discete Time Fourier Transform .
A discrete periodic signal is completely defined by its values in one period, such as the interval [0,N].Any aperiodic signal can be defined as an infinite sum of periodic functions, a useful definition that makes it possible to use Fourier Analysis on it by assuming all frequencies are present in the signal.

Notification Switch
Would you like to follow the 'Signals and systems' conversation and receive update notifications?