| << Chapter < Page | Chapter >> Page > |
where , and are as just defined, and α is given by
The validity of these simplified formulas depends on a number of assumptions, detailed in [link] , but all of them are sufficiently satisfied in this case to permit accuracy in the estimation of L within 5% or so.
Examination of [link] shows that , the filter transition band, can be no larger than , the difference between the channel spacing and the bandwidth of each channel. Recalling also that , we find that
Thus, to first order, the pulse response duration of the required filter is proportional to the number of channels N and is hyperbolic in the percentage bandwidth , the ratio of the channel bandwidth B to the channel spacing . The effect of the proportionality to α will be examined shortly.
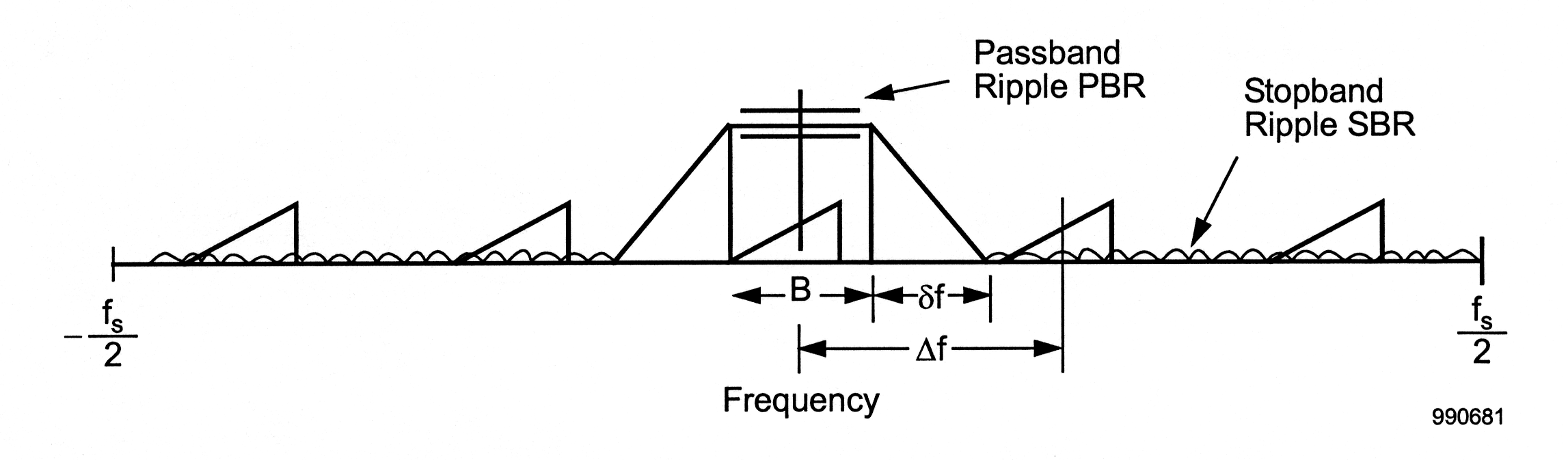
The development presented in the section Derivation of the equations for a Basic FDM-TDM Transmux defined the integer variable Q as the ratio of L and N . It was pointed out there without proof that in fact Q was an important design parameter, not just the artifact of two others. This can now be seen by combining the relationship with [link] to produce an expression for Q :
Since N depends strictly on the number of channels into which the input band is divided, Q contains all of the information about the impact of the desired filter characteristics.
Consider again the example of demodulating R.35 FDM FSK VFT canals discussed in the section Example: Using an FDM-TDM Transmux to Demodulate R.35 Telegraphy Signals . In that section, we determined that the following parameters would be appropriate: Hz, , and Hz. To determine Q , and hence the rate of computation needed for the data weighting segment of the transmultiplexer, we need to specify B and , the degree of stopband suppression required.
Generally speaking, the filters in an FSK demodulator need to have unity gain at the mark or space frequency and zero gain at the space or mark frequency, respectively. A computer simulation used to verify the design of the demodulator showed that suppression of 50 dB was more than enough to provide the needed performance. At first glance it might appear that the transition band can be allowed to equal the tone spacing Hz, making the percentage bandwidth equal to zero. Actual FSK VFT systems, however, sometimes experience bulk frequency shifts of several Hertz. In order to maintain full performance in the presence of such frequency offsets, the tuner filters need to be designed with a passband bandwidth of 15 Hz or so. Using dB in [link] , we find with [link] that the required value of Q for this application is about 2.71. The actual value chosen for this application was 3, producing a pulse response duration of , with the remaining degrees of freedom in the filter design used to widen the filter still more, allowing for even more frequency offset.

Notification Switch
Would you like to follow the 'An introduction to the fdm-tdm digital transmultiplexer' conversation and receive update notifications?