| << Chapter < Page | Chapter >> Page > |
To summarize, we will rewrite [link] according to this interpretation.First, we define two new point data sequences and , which contain the even and odd-numbered datapoints from the original point sequence, respectively:
where . This separation of even and odd points is called decimation in time . The point DFT of is then given by
where and are the point DFT's of the even and odd points.
While [link] requires less computation than the original point DFT, it can still be further simplified.First, note that each point DFT is periodic with period . This means that we need to only compute and for values of rather than the values shown in [link] . Furthermore, the complex exponential factor has the property that
These two facts may be combined to yield a simpler expression for the point DFT:
where the complex constants defined by are commonly known as the twiddle factors .
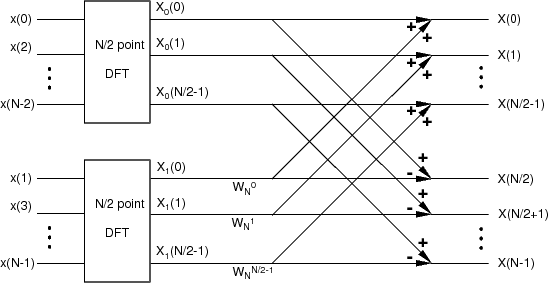
[link] shows a graphical interpretation of [link] which we will refer to as the “divide-and-conquer DFT”. We start on the left side with the data separated intoeven and odd subsets. We perform an point DFT on each subset, and then multiply the output of the odd DFT by the required twiddlefactors. The first half of the output is computed by addingthe two branches, while the second half is formed by subtraction.This type of flow diagram is conventionally used to describe a fast Fourier transform algorithm.
In this section, you will implement the DFT transformationusing [link] and the illustration in [link] . Write a Matlab function with the syntax
X = dcDFT(x)
where
x is a vector of even length
,
and
X is its DFT.
Your function
dcDFT should do the following:
x0 = x(1:2:N) can be used to obtain the “even” points.DFTsum to compute the two
point DFT's.Test your function
dcDFT by using it to compute the DFT's
of the following signals.
dcDFT .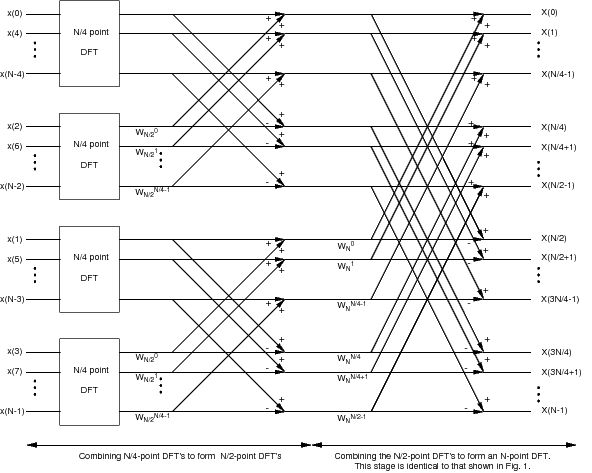
The second basic concept underlying the FFT algorithm is that of recursion. Suppose is also even. Then we may apply the same decimation-in-timeidea to the computation of each of the point DFT's in [link] . This yields the process depicted in [link] . We now have two stages of twiddle factorsinstead of one.
How many times can we repeat the process of decimating the input sequence? Suppose is a power of 2, i.e. for some integer . We can thenrepeatedly decimate the sequence until each subsequence contains only two points.It is easily seen from [link] that the 2 point DFT is a simple sum and difference of values.
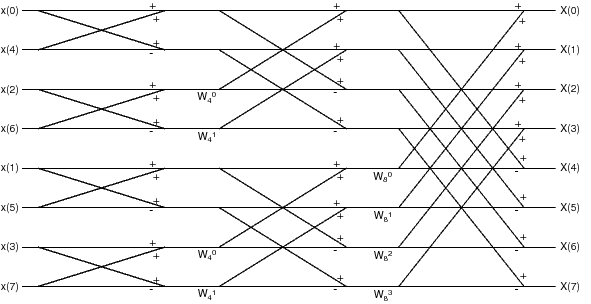
[link] shows the flow diagram that results for an 8 point DFT when we decimate 3 times.Note that there are 3 stages of twiddle factors (in the first stage, the twiddle factors simplify to “1”).This is the flow diagram for the complete decimation-in-time 8 point FFT algorithm.How many multiplies are required to compute it?
Write three Matlab functions to compute the 2, 4, and 8 point FFT's using the syntax
X = FFT2(x)
X = FFT4(x)
X = FFT8(x)
The function
FFT2 should directly compute
the 2-point DFT using
[link] ,
but the functions
FFT4 and
FFT8 should compute their respective FFT's using the divide and
conquer strategy.This means that
FFT8 should call
FFT4 ,
and
FFT4 should call
FFT2 .
Test your function
FFT8 by using it to compute the DFT's
of the following signals. Compare these results to the previous ones.
FFT2 ,
FFT4 and
FFT8 .FFT8 for the case
for
.If you wrote the FFT4 and FFT8 functions properly, they should have almost the exact same form. The only difference between them is the length of the input signal,and the function called to compute the (N/2)-pt DFTs. Obviously, it's redundant to write a separate function for each specificlength DFT when they each have the same form. The preferred method is to write a recursive function, which means that the function calls itself within the body. It is imperative that a recursive function has a condition for exiting withoutcalling itself, otherwise it would never terminate.
Write a recursive function
X=fft_stage(x) that performs one
stage of the FFT algorithm for a power-of-2 length signal.An outline of the function is as follows:
Note that the body of this function should look very similar to previous functions written in this lab.Test fft_stage on the three 8-pt signals given above, and verify that it returns the same results as FFT8 .

Notification Switch
Would you like to follow the 'Purdue digital signal processing labs (ece 438)' conversation and receive update notifications?