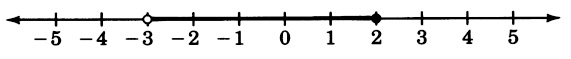means
since the parentheses indicate that the exponent 3 is directly connected to the factor
. Remember that the grouping symbols
indicate that the quantities inside are to be considered as one single number.
means
since the exponent 2 applies only to the factor
.
Practice set b
Write each of the following without exponents.
Sample set c
Select a number to show that
is not always equal to
.
Suppose we choose
to be 5. Consider both
and
.
Notice that
only when
.
Practice set c
Select a number to show that
is not always equal to
.
Select
. Then
, but
.
.
Reading exponential notation
In
,
Base
is the
base
Exponent
is the
exponent
Power
The number represented by
is called a
power .
To the
Th power
The term
is read as "
to the
th power," or more simply as "
to the
th."
Squared and
Cubed
The symbol
is often read as "
squared," and
is often read as "
cubed." A natural question is "Why are geometric terms appearing in the exponent expression?" The answer for
is this:
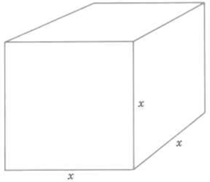
means
. In geometry, the volume of a
rectangular box is found by multiplying the length by the width by the depth. A cube has the same length on each side. If we represent this length by the letter
then the volume of the cube is
, which, of course, is described by
. (Can you think of why
is read as
squared?)
Cube with
length
width
depth
Volume
The order of operations
In Section
[link] we were introduced to the order of operations. It was noted that we would insert another operation before multiplication and division. We can do that now.
The order of operations
- Perform all operations inside grouping symbols beginning with the innermost set.
- Perform all exponential
operations as you come to them, moving left-to-right.
- Perform all multiplications and divisions as you come to them, moving left-to-right.
- Perform all additions and subtractions as you come to them, moving left-to-right.
Sample set d
Use the order of operations to simplify each of the following.
Practice set d
Use the order of operations to simplify the following.
Exercises
For the following problems, write each of the quantities using exponential notation.
3 squared times
to the fifth
cubed minus
squared
cubed plus
to the seventh
For the following problems, expand the quantities so that no exponents appear.
For the following problems, select a number (or numbers) to show that
is not generally equal to
.
is not generally equal to
.
Select
Then,
is not generally equal to
.
For what real number is
equal to
?
For what real numbers,
and
, is
equal to
?
Use the order of operations to simplify the quantities for the following problems.
Exercises for review
(
[link] ) Use algebraic notation to write the statement "a number divided by eight, plus five, is equal to ten."
(
[link] ) Draw a number line that extends from
to 5 and place points at all real numbers that are strictly greater than
but less than or equal to 2.
(
[link] ) Is every integer a whole number?
(
[link] ) Use the commutative property of multiplication to write a number equal to the number
.
(
[link] ) Use the distributive property to expand
.