| << Chapter < Page | Chapter >> Page > |
Therefore, to avoid any aliasing or distortion of the discrete signal frequency content and to be able to recover or reconstruct the frequency content of the original analog signal, we must have . This is known as the Nyquist rate. The sampling frequency should be at least twice the highest frequency in the analog signal. Normally, before any digital manipulation, a front-end anti-aliasing lowpass analog filter is used to limit the highest frequency of the analog signal.
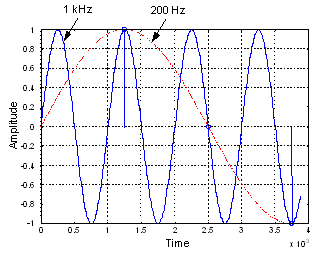
Let us further examine the aliasing problem by considering an undersampled sinusoid as depicted in [link] . In this figure, a 1 kHz sinusoid is sampled at kHz, which is less than the Nyquist rate of 2 kHz. The dashed-line signal is a 200 Hz sinusoid passing through the same sample points. Thus, at the sampling frequency of 0.8 kHz, the output of an A/D converter is the same if one uses the 1 kHz or 200 Hz sinusoid as the input signal. On the other hand, oversampling a signal provides a richer description than that of the signal sampled at the Nyquist rate.
An A/D converter has a finite number of bits (or resolution). As a result, continuous amplitude values get represented or approximated by discrete amplitude levels. The process of converting continuous into discrete amplitude levels is called quantization. This approximation leads to errors called quantization noise. The input/output characteristic of a 3-bit A/D converter is shown in [link] to illustrate how analog voltage values are approximated by discrete voltage levels.
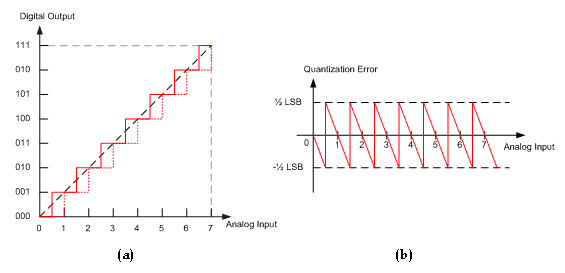
Quantization interval depends on the number of quantization or resolution levels, as illustrated in [link] . Clearly the amount of quantization noise generated by an A/D converter depends on the size of the quantization interval. More quantization bits translate into a narrower quantization interval and, hence, into a lower amount of quantization noise.

In [link] , the spacing Δ between two consecutive quantization levels corresponds to one least significant bit (LSB). Usually, it is assumed that quantization noise is signal-independent and is uniformly distributed over –0.5 LSB and 0.5 LSB. [link] also shows the quantization noise of an analog signal quantized by a 3-bit A/D converter and the corresponding bit stream.
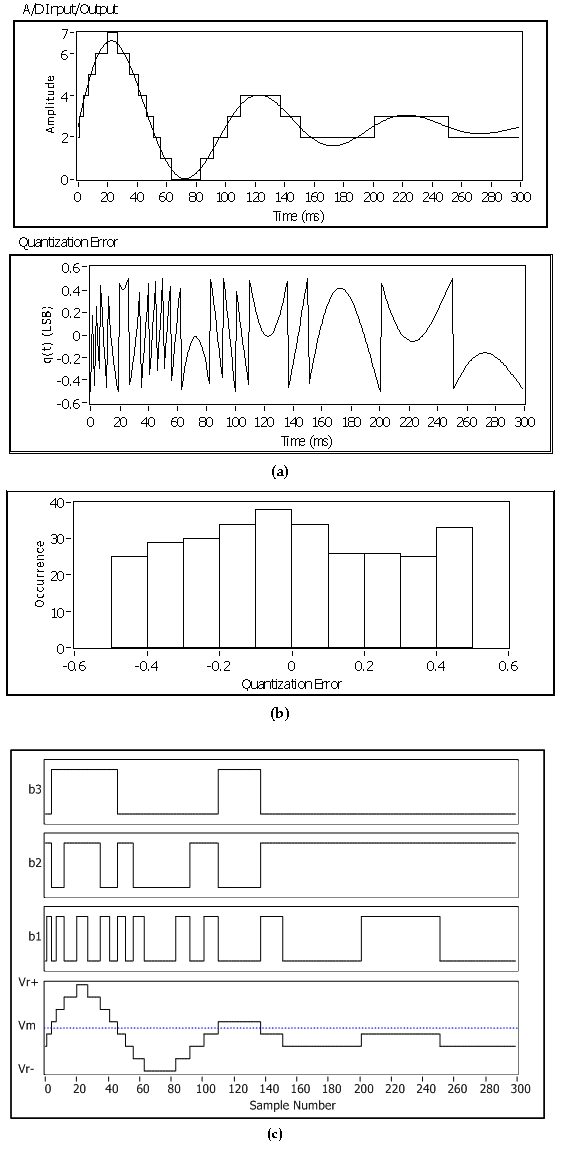
Because it is not possible to have an actual analog signal within a computer programming environment, an analog sinusoidal signal is often simulated by sampling it at a very high sampling frequency. Consider the following analog sine wave:
Sample this sine wave at 40 kHz to generate 0.125 seconds of . Note that the sampling interval,seconds, is very short, so appears as an analog signal.
Sampling involves taking samples from an analog signal everyseconds. The above example generates a discrete signal by taking one sample from the analog signal everyseconds. To get a digital signal, apply quantization to the discrete signal.
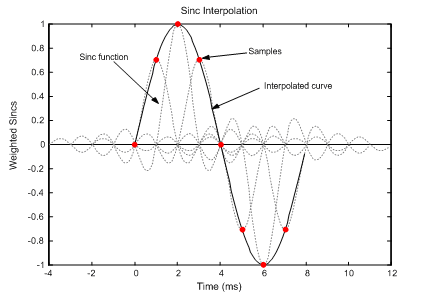
According to the Nyquist theorem, an analog signal z can be reconstructed from its samples by using the following equation:
This reconstruction is based on the summations of shifted sinc (sinx/x) functions. [link] illustrates the reconstruction of a sine wave from its samples achieved in this manner.
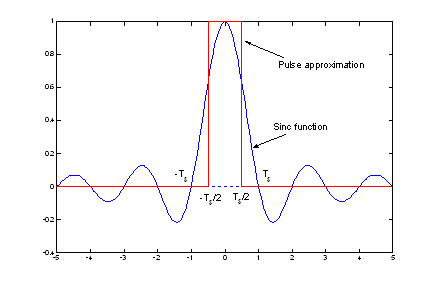
It is difficult to generate sinc functions by electronic circuitry. That is why, in practice, one uses an approximation of a sinc function. [link] shows an approximation of a sinc function by a pulse, which is easy to realize in electronic circuitry. In fact, the well-known sample and hold circuit performs this approximation.
Fourier transformation pairs for analog and discrete signals are expressed in [link] . Note that the discrete-time Fourier transform (DTFT) for discrete-time signals is the counterpart to the continuous-time Fourier transform (CTFT) for continuous-time signals. Also, the discrete Fourier transform (DFT) is the counterpart to the Fourier series (FS) for continuous-time signals as shown in [link] . [link] shows a list of these transformations and their behavior in the time and frequency domains.
| Fourier series for periodic analog signals | , where T denotes period andω 0 fundamental frequency |
| Discrete Fourier transform (DFT) for periodic discrete signals |
| Time domain | Spectrum characteristics | Transformation type |
| Continuous (periodic) | Discrete | FS |
| Continuous (aperiodic) | Continuous | CTFT |
| Discrete (periodic) | Discrete (periodic) | DFT |
| Discrete (aperiodic) | Continuous (periodic) | DTFT |

Notification Switch
Would you like to follow the 'An interactive approach to signals and systems laboratory' conversation and receive update notifications?