| << Chapter < Page | Chapter >> Page > |
Sketch or use a graphing tool to view the graph of the cylindrical surface defined by equation
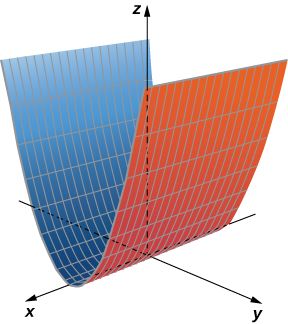
When sketching surfaces, we have seen that it is useful to sketch the intersection of the surface with a plane parallel to one of the coordinate planes. These curves are called traces. We can see them in the plot of the cylinder in [link] .
The traces of a surface are the cross-sections created when the surface intersects a plane parallel to one of the coordinate planes.
Traces are useful in sketching cylindrical surfaces. For a cylinder in three dimensions, though, only one set of traces is useful. Notice, in [link] , that the trace of the graph of in the xz -plane is useful in constructing the graph. The trace in the xy -plane, though, is just a series of parallel lines, and the trace in the yz -plane is simply one line.
Cylindrical surfaces are formed by a set of parallel lines. Not all surfaces in three dimensions are constructed so simply, however. We now explore more complex surfaces, and traces are an important tool in this investigation.
We have learned about surfaces in three dimensions described by first-order equations; these are planes. Some other common types of surfaces can be described by second-order equations. We can view these surfaces as three-dimensional extensions of the conic sections we discussed earlier: the ellipse, the parabola, and the hyperbola. We call these graphs quadric surfaces.
Quadric surfaces are the graphs of equations that can be expressed in the form
When a quadric surface intersects a coordinate plane, the trace is a conic section.
An ellipsoid is a surface described by an equation of the form Set to see the trace of the ellipsoid in the yz -plane. To see the traces in the y - and xz -planes, set and respectively. Notice that, if the trace in the xy -plane is a circle. Similarly, if the trace in the xz -plane is a circle and, if then the trace in the yz -plane is a circle. A sphere, then, is an ellipsoid with
Sketch the ellipsoid
Start by sketching the traces. To find the trace in the xy -plane, set (see [link] ). To find the other traces, first set and then set

Now that we know what traces of this solid look like, we can sketch the surface in three dimensions ( [link] ).
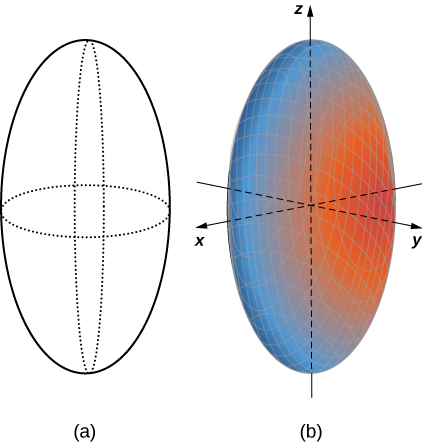
The trace of an ellipsoid is an ellipse in each of the coordinate planes. However, this does not have to be the case for all quadric surfaces. Many quadric surfaces have traces that are different kinds of conic sections, and this is usually indicated by the name of the surface. For example, if a surface can be described by an equation of the form then we call that surface an elliptic paraboloid . The trace in the xy -plane is an ellipse, but the traces in the xz -plane and yz -plane are parabolas ( [link] ). Other elliptic paraboloids can have other orientations simply by interchanging the variables to give us a different variable in the linear term of the equation or

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?