| << Chapter < Page | Chapter >> Page > |
This chapter forms the basis of the discussion into mechanical waves. Waves are all around us, even though most of us are not aware of it. The most common waves are waves in the sea, but waves can be created in any container of water, ranging from an ocean to a tea-cup. Waves do not only occur in water, they occur in any kind of medium. Earthquakes generate waves that travel through the rock of the Earth. When your friend speaks to you he produces sound waves that travel through the air to your ears. Light is made up of electromagnetic waves. A wave is simply moving energy.
In this chapter, as well as in the following chapters, we will speak about waves moving in a medium. A medium is just the substance or material through which waves move. In other words the medium carries the wave from one place to another. The medium does not create the wave and the medium is not the wave. Therefore the medium does not travel with the wave as the wave propagates through it. Air is a medium for sound waves, water is a medium for water waves and rock is a medium for earthquakes (which are also a type of wave). Air, water and rock are therefore examples of media (media is the plural of medium).
A medium is the substance or material in which a wave will move.
In each medium, the atoms that make up the medium are moved temporarily from their rest position. In order for a wave to travel, the different parts of the medium must be able to interact with each other.
Take a heavy rope. Have two people hold the rope stretched out horizontally. Flick the rope at one end only once.

What happens to the disturbance that you created in the rope? Does it stay at the place where it was created or does it move down the length of the rope?
In the activity, we created a pulse . A pulse is a single disturbance that moves through a medium. In a transverse pulse the displacement of the medium is perpendicular to the direction of motion of the pulse. [link] shows an example of a transverse pulse. In the activity, the rope or spring was held horizontally and the pulse moved the rope up and down. This was an example of a transverse pulse.
A pulse is a single disturbance that moves through a medium.
A pulse where all of the particles disturbed by the pulse move perpendicular (at a right angle) to the direction in which the pulse is moving.
The amplitude of a pulse is a measurement of how far the medium is displaced momentarily from a position of rest. The pulse length is a measurement of how long the pulse is. Both these quantities are shown in [link] .
The amplitude of a pulse is a measurement of how far the medium is displaced from rest.

The position of rest is the position the medium would be in if it were undisturbed. This is also called the equilibrium position. Sometimes people will use rest and sometimes equilibrium but they will also use to the two in the same discussion to mean the same thing.
The graphs below show the positions of a pulse at different times.
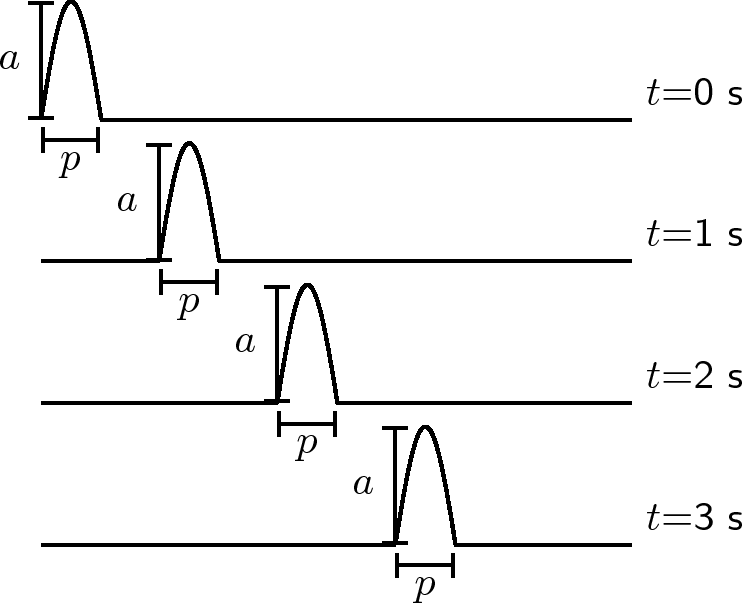
Use your ruler to measure the lengths of and . Fill your answers in the table.
| Time | ||
| s | ||
| s | ||
| s | ||
| s |
What do you notice about the values of and ?
In the activity, we found that the values for how high the pulse ( ) is and how wide the pulse ( ) is the same at different times. Pulse length and amplitude are two important quantities of a pulse.
Pulse speed is the distance a pulse travels per unit time.
In Motion in one dimension we saw that speed was defined as the distance traveled per unit time. We can use the same definition of speed to calculate how fast a pulse travels. If the pulse travels a distance in a time , then the pulse speed is:
A pulse covers a distance of in on a heavy rope. Calculate the pulse speed.
We are given:
We are required to calculate the speed of the pulse.
We can use:
to calculate the speed of the pulse.
The pulse speed is .

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 physical science [caps]' conversation and receive update notifications?