| << Chapter < Page | Chapter >> Page > |
We already examined exponential functions and logarithms in earlier chapters. However, we glossed over some key details in the previous discussions. For example, we did not study how to treat exponential functions with exponents that are irrational. The definition of the number e is another area where the previous development was somewhat incomplete. We now have the tools to deal with these concepts in a more mathematically rigorous way, and we do so in this section.
For purposes of this section, assume we have not yet defined the natural logarithm, the number e , or any of the integration and differentiation formulas associated with these functions. By the end of the section, we will have studied these concepts in a mathematically rigorous way (and we will see they are consistent with the concepts we learned earlier).
We begin the section by defining the natural logarithm in terms of an integral. This definition forms the foundation for the section. From this definition, we derive differentiation formulas, define the number and expand these concepts to logarithms and exponential functions of any base.
Recall the power rule for integrals:
Clearly, this does not work when as it would force us to divide by zero. So, what do we do with Recall from the Fundamental Theorem of Calculus that is an antiderivative of Therefore, we can make the following definition.
For define the natural logarithm function by
For this is just the area under the curve from to For we have so in this case it is the negative of the area under the curve from (see the following figure).
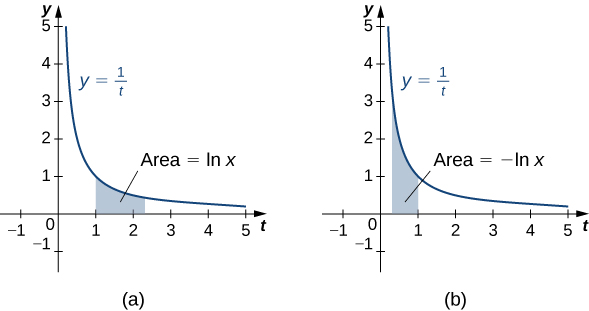
Notice that Furthermore, the function for Therefore, by the properties of integrals, it is clear that is increasing for
Because of the way we defined the natural logarithm, the following differentiation formula falls out immediately as a result of to the Fundamental Theorem of Calculus.
For the derivative of the natural logarithm is given by
The function is differentiable; therefore, it is continuous.
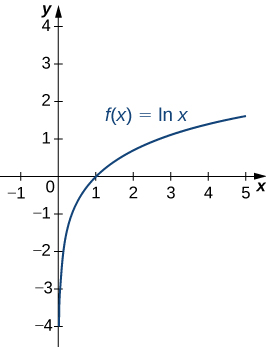
A graph of is shown in [link] . Notice that it is continuous throughout its domain of

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?