2.4 The cross product (Page 2/16)

Page 2 / 16

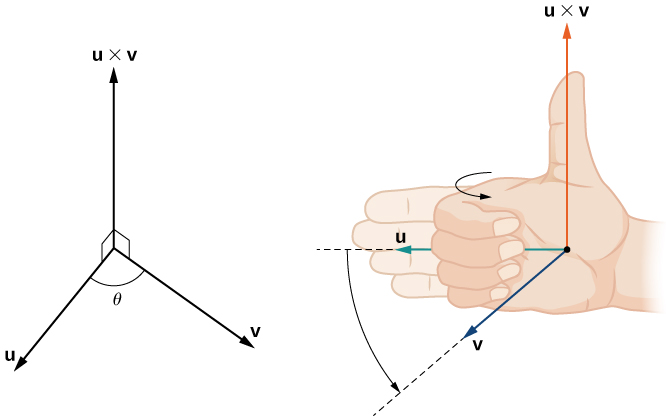
This figure has two images. The first image has three vectors with the same initial point. Two of the vectors are labeled “u” and “v.” The angle between u and v is theta. The third vector is perpendicular to u and v. It is labeled “u cross v.” The second image has three vectors. The vectors are labeled “u, v, and u cross v.” “u cross v” is perpendicular to u and v. Also, on the image of these three vectors is a right hand. The fingers are in the direction of u. As the hand is closing, the direction of the closing fingers is the direction of v. The thumb is up and in the direction of “u cross v.” — The direction of $u \times v$ is determined by the right-hand rule.

Notice what this means for the direction of $v \times u .$ If we apply the right-hand rule to $v \times u,$ we start with our fingers pointed in the direction of $v,$ then curl our fingers toward the vector $u .$ In this case, the thumb points in the opposite direction of $u \times v .$ (Try it!)

Anticommutativity of the cross product

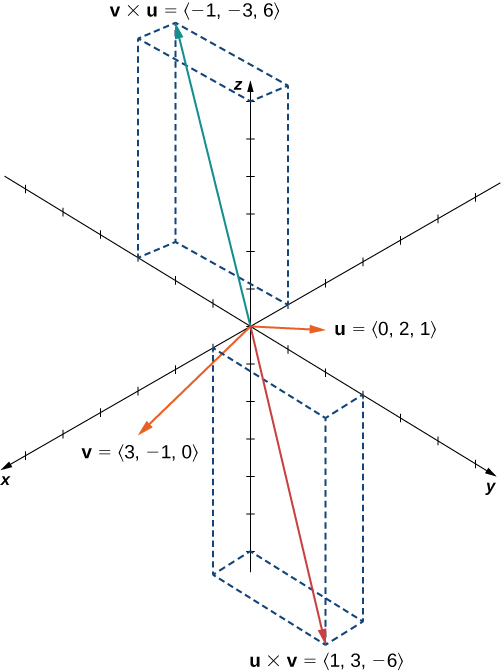
Let $u = ⟨ 0, 2, 1 ⟩$ and $v = ⟨ 3, −1, 0 ⟩ .$ Calculate $u \times v$ and $v \times u$ and graph them.

This figure is the 3-dimensional coordinate system. It has two vectors in standard position. The first vector is labeled “u = <0, 2, 1>.” The second vector is labeled “v = <3, -1, 0>.” — Are the cross products $u \times v$ and $v \times u$ in the same direction?

We have

\begin{matrix} u \times v & = & ⟨ (0 + 1), − (0 - 3), (0 - 6) ⟩ = ⟨ 1, 3, −6 ⟩ \\ v \times u & = & ⟨ (−1 - 0), − (3 - 0), (6 - 0) ⟩ = ⟨ −1, −3, 6 ⟩ . \end{matrix}

We see that, in this case, $u \times v = − (v \times u)$ ( [link] ). We prove this in general later in this section.

Got questions? Get instant answers now!

Suppose vectors $u$ and $v$ lie in the xy -plane (the z -component of each vector is zero). Now suppose the x - and y -components of $u$ and the y -component of $v$ are all positive, whereas the x -component of $v$ is negative. Assuming the coordinate axes are oriented in the usual positions, in which direction does $u \times v$ point?

Up (the positive z -direction)

Got questions? Get instant answers now!

The cross products of the standard unit vectors $i, j,$ and $k$ can be useful for simplifying some calculations, so let’s consider these cross products. A straightforward application of the definition shows that

i \times i = j \times j = k \times k = 0 .

(The cross product of two vectors is a vector, so each of these products results in the zero vector, not the scalar $0 .)$ It’s up to you to verify the calculations on your own.

Furthermore, because the cross product of two vectors is orthogonal to each of these vectors, we know that the cross product of $i$ and $j$ is parallel to $k .$ Similarly, the vector product of $i$ and $k$ is parallel to $j,$ and the vector product of $j$ and $k$ is parallel to $i .$ We can use the right-hand rule to determine the direction of each product. Then we have

\begin{matrix} i \times j & = & k & j \times i & = & − k \\ j \times k & = & i & k \times j & = & − i \\ k \times i & = & j & i \times k & = & − j . \end{matrix}

These formulas come in handy later.

Cross product of standard unit vectors

Find $i \times (j \times k) .$

We know that $j \times k = i .$ Therefore, $i \times (j \times k) = i \times i = 0 .$

Got questions? Get instant answers now!

Find $(i \times j) \times (k \times i) .$

$− i$

Got questions? Get instant answers now!

As we have seen, the dot product is often called the scalar product because it results in a scalar. The cross product results in a vector, so it is sometimes called the vector product . These operations are both versions of vector multiplication, but they have very different properties and applications. Let’s explore some properties of the cross product. We prove only a few of them. Proofs of the other properties are left as exercises.

Properties of the cross product

Let $u, v,$ and $w$ be vectors in space, and let $c$ be a scalar.

\begin{matrix} i. & u \times v & = & − (v \times u) & Anticommutative property \\ ii. & u \times (v + w) & = & u \times v + u \times w & Distributive property \\ iii. & c (u \times v) & = & (c u) \times v = u \times (c v) & Multiplication by a constant \\ iv. & u \times 0 & = & 0 \times u = 0 & Cross product of the zero vector \\ v. & v \times v & = & 0 & Cross product of a vector with itself \\ vi. & u \cdot (v \times w) & = & (u \times v) \cdot w & Scalar triple product \end{matrix}

Proof

For property $i .,$ we want to show $u \times v = − (v \times u) .$ We have

\begin{matrix} u \times v & = ⟨ u_{1}, u_{2}, u_{3} ⟩ \times ⟨ v_{1}, v_{2}, v_{3} ⟩ \\ = ⟨ u_{2} v_{3} - u_{3} v_{2}, − u_{1} v_{3} + u_{3} v_{1}, u_{1} v_{2} - u_{2} v_{1} ⟩ \\ = − ⟨ u_{3} v_{2} - u_{2} v_{3}, − u_{3} v_{1} + u_{1} v_{3}, u_{2} v_{1} - u_{1} v_{2} ⟩ \\ = − ⟨ v_{1}, v_{2}, v_{3} ⟩ \times ⟨ u_{1}, u_{2}, u_{3} ⟩ \\ = − (v \times u) . \end{matrix}

Unlike most operations we’ve seen, the cross product is not commutative. This makes sense if we think about the right-hand rule.

<< Chapter < Page Page > Chapter >>

Practice Key Terms 6

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Calculus volume 3. OpenStax CNX. Feb 05, 2016 Download for free at http://legacy.cnx.org/content/col11966/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?

Ask

	Lean Startup Quiz By Yasser Ibrahim Start Quiz
	4 Microbiology Final 4 By Madison Christian Start Quiz
	Introduction to sociology 2e By OpenStax Read Online Course
	28 AP 28 Development Inheritance Essay By OpenStax Start Flashcards
	3 Understanding Societies MCQ By Jessica Collett Start Quiz
	2 Understanding Societies 2 By Jessica Collett Start Exam
	4 Microeconomics 04 Labor Financial Markets By OpenStax Start Flashcards
	Anatomy & Physiology By OpenStax Read Online Course
	2 Week 2 Social Psych By Yacoub Jayoghli Start Quiz
	Capitalism Market Economy By Robert Murphy Start Test