1. Home
  2. Calculus volume 3
  3. Vectors in space
  4. The dot product

2.3 The dot product  (Page 5/16)

<< Chapter < Page
  Calculus volume 3     Page 5 / 16
Chapter >> Page >

On June 1, AAA Party Supply Store decided to increase the price they charge for party favors to $2 per package. They also changed suppliers for their invitations, and are now able to purchase invitations for only 10¢ per package. All their other costs and prices remain the same. If AAA sells 1408 invitations, 147 party favors, 2112 decorations, and 1894 food service items in the month of June, use vectors and dot products to calculate their total sales and profit for June.

Sales = $15,685.50; profit = $14,073.15

Got questions? Get instant answers now!

Projections

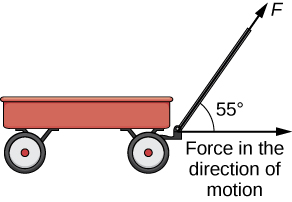
As we have seen, addition combines two vectors to create a resultant vector. But what if we are given a vector and we need to find its component parts? We use vector projections to perform the opposite process; they can break down a vector into its components. The magnitude of a vector projection is a scalar projection. For example, if a child is pulling the handle of a wagon at a 55° angle, we can use projections to determine how much of the force on the handle is actually moving the wagon forward ( [link] ). We return to this example and learn how to solve it after we see how to calculate projections.

This figure is the image of a wagon with a handle. The handle is represented by the vector “F.” The angle between F and the horizontal direction of the wagon is 55 degrees.
When a child pulls a wagon, only the horizontal component of the force propels the wagon forward.

Definition

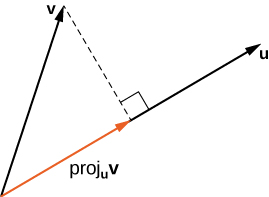
The vector projection    of v onto u is the vector labeled proj u v in [link] . It has the same initial point as u and v and the same direction as u , and represents the component of v that acts in the direction of u . If θ represents the angle between u and v , then, by properties of triangles, we know the length of proj u v is ‖ proj u v ‖ = ‖ v ‖ cos θ . When expressing cos θ in terms of the dot product, this becomes

‖ proj u v ‖ = ‖ v ‖ cos θ = ‖ v ‖ ( u · v ‖ u ‖ ‖ v ‖ ) = u · v ‖ u ‖ .

We now multiply by a unit vector in the direction of u to get proj u v :

proj u v = u · v ‖ u ‖ ( 1 ‖ u ‖ u ) = u · v ‖ u ‖ 2 u .

The length of this vector is also known as the scalar projection    of v onto u and is denoted by

‖ proj u v ‖ = comp u v = u · v ‖ u ‖ .
This image has a vector labeled “v.” There is also a vector with the same initial point labeled “proj sub u v.” The third vector is from the terminal point of proj sub u v in the same direction labeled “u.” A broken line segment from the initial point of u to the terminal point of v is drawn and is perpendicular to u.
The projection of v onto u shows the component of vector v in the direction of u .

Finding projections

Find the projection of v onto u.

  1. v = ⟨ 3 , 5 , 1 ⟩ and u = ⟨ −1 , 4 , 3 ⟩
  2. v = 3 i − 2 j and u = i + 6 j
  1. Substitute the components of v and u into the formula for the projection:
    proj u v = u · v ‖ u ‖ 2 u = ⟨ −1 , 4 , 3 ⟩ · ⟨ 3 , 5 , 1 ⟩ ‖ ⟨ −1 , 4 , 3 ⟩ ‖ 2 ⟨ −1 , 4 , 3 ⟩ = −3 + 20 + 3 ( −1 ) 2 + 4 2 + 3 2 ⟨ −1 , 4 , 3 ⟩ = 20 26 ⟨ −1 , 4 , 3 ⟩ = ⟨ − 10 13 , 40 13 , 30 13 ⟩ .
  2. To find the two-dimensional projection, simply adapt the formula to the two-dimensional case:
    proj u v = u · v ‖ u ‖ 2 u = ( i + 6 j ) · ( 3 i − 2 j ) ‖ i + 6 j ‖ 2 ( i + 6 j ) = 1 ( 3 ) + 6 ( −2 ) 1 2 + 6 2 ( i + 6 j ) = − 9 37 ( i + 6 j ) = − 9 37 i − 54 37 j .
Got questions? Get instant answers now!
Got questions? Get instant answers now!

Sometimes it is useful to decompose vectors—that is, to break a vector apart into a sum. This process is called the resolution of a vector into components . Projections allow us to identify two orthogonal vectors having a desired sum. For example, let v = ⟨ 6 , −4 ⟩ and let u = ⟨ 3 , 1 ⟩ . We want to decompose the vector v into orthogonal components such that one of the component vectors has the same direction as u .

We first find the component that has the same direction as u by projecting v onto u . Let p = proj u v . Then, we have

p = u · v ‖ u ‖ 2 u = 18 − 4 9 + 1 u = 7 5 u = 7 5 ⟨ 3 , 1 ⟩ = ⟨ 21 5 , 7 5 ⟩ .

Now consider the vector q = v − p . We have

q = v − p = ⟨ 6 , −4 ⟩ − ⟨ 21 5 , 7 5 ⟩ = ⟨ 9 5 , − 27 5 ⟩ .

Clearly, by the way we defined q , we have v = q + p , and
<< Chapter < Page Page > Chapter >>
Practice Key Terms 7

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Calculus volume 3. OpenStax CNX. Feb 05, 2016 Download for free at http://legacy.cnx.org/content/col11966/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?

Ask