| << Chapter < Page | Chapter >> Page > |
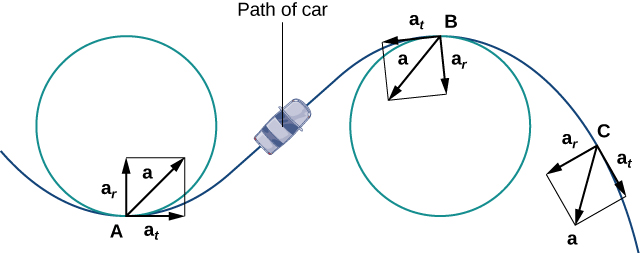
The normal component of acceleration is also called the centripetal component of acceleration or sometimes the radial component of acceleration . To understand centripetal acceleration, suppose you are traveling in a car on a circular track at a constant speed. Then, as we saw earlier, the acceleration vector points toward the center of the track at all times. As a rider in the car, you feel a pull toward the outside of the track because you are constantly turning. This sensation acts in the opposite direction of centripetal acceleration. The same holds true for noncircular paths. The reason is that your body tends to travel in a straight line and resists the force resulting from acceleration that push it toward the side. Note that at point B in [link] the acceleration vector is pointing backward. This is because the car is decelerating as it goes into the curve.
The tangential and normal unit vectors at any given point on the curve provide a frame of reference at that point. The tangential and normal components of acceleration are the projections of the acceleration vector onto T and N , respectively.
A particle moves in a path defined by the vector-valued function where t measures time in seconds and distance is measured in feet.
An object moves in a path defined by the vector-valued function where t measures time in seconds.
Now let’s look at an application of vector functions. In particular, let’s consider the effect of gravity on the motion of an object as it travels through the air, and how it determines the resulting trajectory of that object. In the following, we ignore the effect of air resistance. This situation, with an object moving with an initial velocity but with no forces acting on it other than gravity, is known as projectile motion . It describes the motion of objects from golf balls to baseballs, and from arrows to cannonballs.
First we need to choose a coordinate system. If we are standing at the origin of this coordinate system, then we choose the positive y -axis to be up, the negative y- axis to be down, and the positive x- axis to be forward (i.e., away from the thrower of the object). The effect of gravity is in a downward direction, so Newton’s second law tells us that the force on the object resulting from gravity is equal to the mass of the object times the acceleration resulting from to gravity, or where represents the force from gravity and g represents the acceleration resulting from gravity at Earth’s surface. The value of g in the English system of measurement is approximately 32 ft/sec 2 and it is approximately 9.8 m/sec 2 in the metric system. This is the only force acting on the object. Since gravity acts in a downward direction, we can write the force resulting from gravity in the form as shown in the following figure.

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?