| << Chapter < Page | Chapter >> Page > |
If the bicycle in the preceding example had been on its wheels instead of upside-down, it would first have accelerated along the ground and then come to a stop. This connection between circular motion and linear motion needs to be explored. For example, it would be useful to know how linear and angular acceleration are related. In circular motion, linear acceleration is tangent to the circle at the point of interest, as seen in [link] . Thus, linear acceleration is called tangential acceleration .
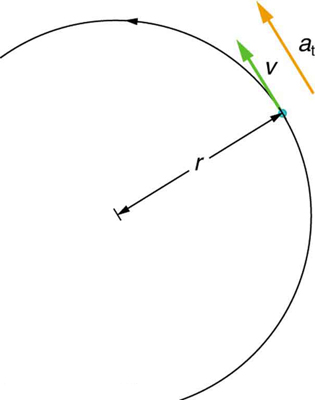
Linear or tangential acceleration refers to changes in the magnitude of velocity but not its direction. We know from Uniform Circular Motion and Gravitation that in circular motion centripetal acceleration, , refers to changes in the direction of the velocity but not its magnitude. An object undergoing circular motion experiences centripetal acceleration, as seen in [link] . Thus, and are perpendicular and independent of one another. Tangential acceleration is directly related to the angular acceleration and is linked to an increase or decrease in the velocity, but not its direction.
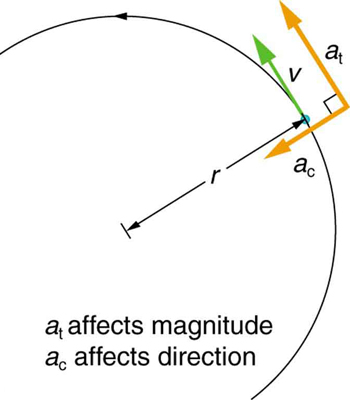
Now we can find the exact relationship between linear acceleration and angular acceleration . Because linear acceleration is proportional to a change in the magnitude of the velocity, it is defined (as it was in One-Dimensional Kinematics ) to be
For circular motion, note that , so that
The radius is constant for circular motion, and so . Thus,
By definition, . Thus,
or
These equations mean that linear acceleration and angular acceleration are directly proportional. The greater the angular acceleration is, the larger the linear (tangential) acceleration is, and vice versa. For example, the greater the angular acceleration of a car’s drive wheels, the greater the acceleration of the car. The radius also matters. For example, the smaller a wheel, the smaller its linear acceleration for a given angular acceleration .
A powerful motorcycle can accelerate from 0 to 30.0 m/s (about 108 km/h) in 4.20 s. What is the angular acceleration of its 0.320-m-radius wheels? (See [link] .)
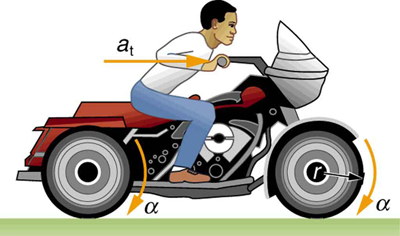
Strategy
We are given information about the linear velocities of the motorcycle. Thus, we can find its linear acceleration . Then, the expression can be used to find the angular acceleration.
Solution
The linear acceleration is
We also know the radius of the wheels. Entering the values for and into , we get
Discussion
Units of radians are dimensionless and appear in any relationship between angular and linear quantities.
So far, we have defined three rotational quantities— , and . These quantities are analogous to the translational quantities , and . [link] displays rotational quantities, the analogous translational quantities, and the relationships between them.
| Rotational | Translational | Relationship |
|---|---|---|
Angular acceleration is a vector, having both magnitude and direction. How do we denote its magnitude and direction? Illustrate with an example.
The magnitude of angular acceleration is and its most common units are . The direction of angular acceleration along a fixed axis is denoted by a + or a – sign, just as the direction of linear acceleration in one dimension is denoted by a + or a – sign. For example, consider a gymnast doing a forward flip. Her angular momentum would be parallel to the mat and to her left. The magnitude of her angular acceleration would be proportional to her angular velocity (spin rate) and her moment of inertia about her spin axis.
or
Analogies exist between rotational and translational physical quantities. Identify the rotational term analogous to each of the following: acceleration, force, mass, work, translational kinetic energy, linear momentum, impulse.
Suppose a piece of food is on the edge of a rotating microwave oven plate. Does it experience nonzero tangential acceleration, centripetal acceleration, or both when: (a) The plate starts to spin? (b) The plate rotates at constant angular velocity? (c) The plate slows to a halt?
At its peak, a tornado is 60.0 m in diameter and carries 500 km/h winds. What is its angular velocity in revolutions per second?
Integrated Concepts
An ultracentrifuge accelerates from rest to 100,000 rpm in 2.00 min. (a) What is its angular acceleration in ? (b) What is the tangential acceleration of a point 9.50 cm from the axis of rotation? (c) What is the radial acceleration in and multiples of of this point at full rpm?
You have a grindstone (a disk) that is 90.0 kg, has a 0.340-m radius, and is turning at 90.0 rpm, and you press a steel axe against it with a radial force of 20.0 N. (a) Assuming the kinetic coefficient of friction between steel and stone is 0.20, calculate the angular acceleration of the grindstone. (b) How many turns will the stone make before coming to rest?
(a)
(b)

Notification Switch
Would you like to follow the 'Unit 8 - rotational motion' conversation and receive update notifications?