| << Chapter < Page | Chapter >> Page > |
We will now study the graphs of quadratic equations in two variables with general form
We will construct the graph of a parabola by choosing several -values, computing to find the corresponding -values, plotting these ordered pairs, then drawing a smooth curve through them.
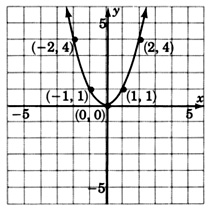
Graph
Construct a table to exhibit several ordered pairs.
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 1 | |
| 4 | |
| 9 |
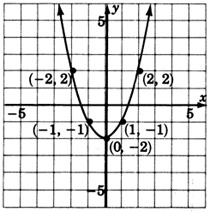
Graph
Construct a table of ordered pairs.
| 0 | |
| 1 | |
| 2 | 2 |
| 3 | 7 |
| 2 | |
| 7 |
Use the idea suggested in Sample Set A to sketch (quickly and perhaps not perfectly accurately) the graphs of

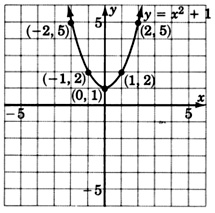
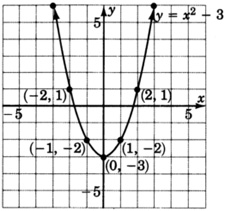
Graph
Do we expect the graph to be similar to the graph of
? Make a table of ordered pairs.
| 0 | 4 |
| 1 | 9 |
| 1 | |
| 0 | |
| 1 | |
| 4 |
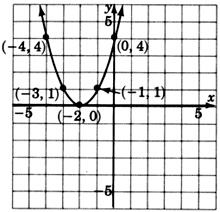
Use the idea suggested in Sample Set B to sketch the graphs of

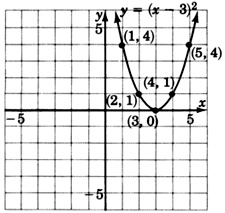
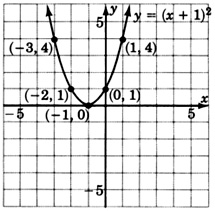
For the following problems, graph the quadratic equations.
(Compare with problem 2.)

For the following problems, try to guess the quadratic equation that corresponds to the given graph.
( [link] ) Simplify and write so that only positive exponents appear.
( [link] ) Find the sum:
( [link] ) Four is added to an integer and that sum is doubled. When this result is multiplied by the original integer, the product is Find the integer.

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?