| << Chapter < Page | Chapter >> Page > |
Suppose a body has a force of 3 pounds acting on it to the left, 4 pounds acting on it upward, and 2 pounds acting on it 30° from the horizontal. What single force is needed to produce a state of equilibrium on the body? Draw the vector.
5.1583 pounds, 75.8° from the horizontal
For the following exercises, assume is opposite side is opposite side and is opposite side Solve each triangle, if possible. Round each answer to the nearest tenth.
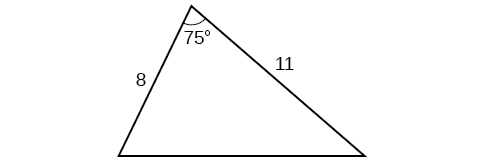
Find the area of the triangle.
A pilot is flying over a straight highway. He determines the angles of depression to two mileposts, 2.1 km apart, to be 25° and 49°, as shown in [link] . Find the distance of the plane from point and the elevation of the plane.
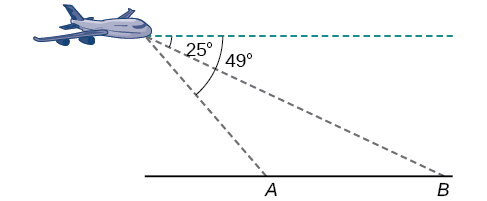
distance of the plane from point 2.2 km, elevation of the plane: 1.6 km
Solve the triangle, rounding to the nearest tenth, assuming is opposite side is opposite side and s opposite side
Solve the triangle in [link] , rounding to the nearest tenth.
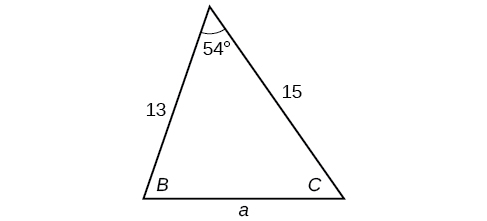
Find the area of a triangle with sides of length 8.3, 6.6, and 9.1.
To find the distance between two cities, a satellite calculates the distances and angle shown in [link] (not to scale). Find the distance between the cities. Round answers to the nearest tenth.
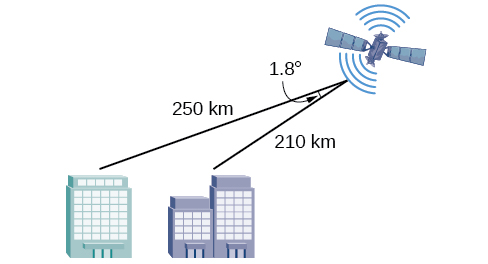
40.6 km
Plot the point with polar coordinates
Convert to rectangular coordinates.
Convert to polar coordinates.
For the following exercises, convert the given Cartesian equation to a polar equation.
For the following exercises, convert the given polar equation to a Cartesian equation.
For the following exercises, convert to rectangular form and graph.
For the following exercises, test each equation for symmetry.
Sketch a graph of the polar equation Label the axis intercepts.
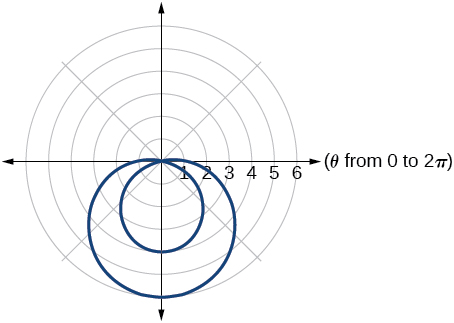
Sketch a graph of the polar equation
For the following exercises, find the absolute value of each complex number.
Write the complex number in polar form.
For the following exercises, convert the complex number from polar to rectangular form.
For the following exercises, find the product in polar form.
For the following exercises, find the quotient in polar form.
For the following exercises, find the powers of each complex number in polar form.
Find when

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?