| << Chapter < Page | Chapter >> Page > |
The amplitude is the maximum displacement of a particle from its equilibrium position.

Fill in the table below by measuring the distance between the equilibrium and each peak and troughs in the wave above. Use your ruler to measure the distances.
| Peak/Trough | Measurement (cm) |
| a | |
| b | |
| c | |
| d | |
| e | |
| f |
As we have seen in the activity on amplitude, the distance between the peak and the equilibrium position is equal to the distance between the trough and the equilibrium position. This distance is known as the amplitude of the wave, and is the characteristic height of wave, above or below the equilibrium position. Normally the symbol is used to represent the amplitude of a wave. The SI unit of amplitude is the metre (m).

If the peak of a wave measures above the still water mark in the harbour, what is the amplitude of the wave?
The definition of the amplitude is the height of a peak above the equilibrium position. The still water mark is the height of the water at equilibrium and the peak is above this, so the amplitude is .
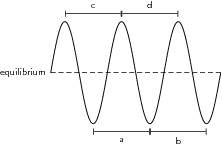
Fill in the table below by measuring the distance between peaks and troughs in the wave above.
| Distance(cm) | |
| a | |
| b | |
| c | |
| d |
As we have seen in the activity on wavelength, the distance between two adjacent peaks is the same no matter which two adjacent peaks you choose. There is a fixed distance between the peaks. Similarly, we have seen that there is a fixed distance between the troughs, no matter which two troughs you look at. More importantly, the distance between two adjacent peaks is the same as the distance between two adjacent troughs. This distance is called the wavelength of the wave.
The symbol for the wavelength is (the Greek letter lambda ) and wavelength is measured in metres ( ).

The total distance between consecutive peaks of a transverse wave is . What is the wavelength of the wave?

From the sketch we see that 4 consecutive peaks is equivalent to 3 wavelengths.
Therefore, the wavelength of the wave is:
Fill in the table by measuring the distance between the indicated points.

| Points | Distance (cm) |
| A to F | |
| B to G | |
| C to H | |
| D to I | |
| E to J |
What do you find?
In the activity the distance between the indicated points was the same. These points are then said to be in phase . Two points in phase are separate by an integer (0,1,2,3,...) number of complete wave cycles. They do not have to be peaks or troughs, but they must be separated by a complete number of wavelengths.

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 physical science' conversation and receive update notifications?