| << Chapter < Page | Chapter >> Page > |
In Graad 10 het ons die idee van gemiddelde gradiënt ondersoek and gesien dat die gradiënt van sommige funksies verskillend is by verskillende intervalle. In Graad 11 kyk ons verder na die idee van gemiddelde gradiënt, en stel die idee van 'n gradiënt van 'n kurwe by 'n punt bekend.
Ons het gesien dat die gemiddelde gradiënt tussen twee punte op 'n kurwe die gradiënt is van die reguitlyn wat deur twee punte gaan.
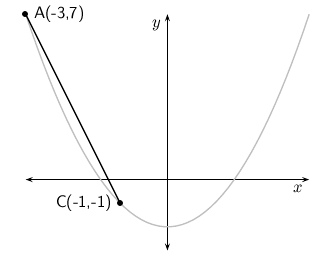
Wat gebeur met die gradiënt as ons die posisie van een punt vasstel en die tweede punt nader aan die vaste punt beweeg?
Die kurwe gewys is gedefineër deur . Punt B is vasgestel by koördinate (0, -5). Die posisie van punt A wissel. Voltooi die tabel hieronder deur die -koördinate van punt A te bereken vir die gegewe -koördinate. Bereken dan die gemiddelde gradiënt tussen punte A en B.
| gemiddelde gradiënt | ||
| -2 | ||
| -1.5 | ||
| -1 | ||
| -0.5 | ||
| 0 | ||
| 0.5 | ||
| 1 | ||
| 1.5 | ||
| 2 |
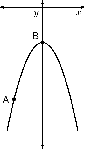
Wat gebeur met die gemiddelde gradiënt soos A in die rigting van B beweeg? Wat gebreur met die gemiddelde gradieënt soos A wegbeweeg van B?Wat is die gemiddelde gradiënt wanneer A oorvleuel met B?
In [link] verander die gradiënt van die reguitlyn wat deur punte A en C gaan soos A nader beweeg aan C. By die punt wat A en C oorvleuel gaan die reguitlyn slegs deur een punt op die kurwe. So 'n lyn is bekend as 'n raaklyn aan die kurwe.
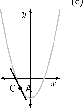

Ons stel dan die idee bekend van 'n gradiënt by 'n enkele punt op 'n kurwe. Die gradiënt by 'n punt op 'n kurwe is eenvoudig die gradiënt van die raaklyn aan die kurwe by die gegewe punt.
Kry die gemiddelde gradiënt tussen twee punte P en Q op die kurwe . Kry dan die gemiddelde gradiënt tussen P en Q . Laastens, verduidelik wat gebeur met die gemiddelde gradiënt soos P nader beweeg aan Q.
Deur die funksie te gebruik, kry ons:
Die gemiddelde gradiënt tussen P en Q op die kurwe is .
Ons kan die resultaat in [link] gebruik, maar ons sal moet bepaal wat en is. Ons doen dit deur te kyk na die definisies van P en Q. Die -koërdinaat van P is en die -koördinaat van Q is . Daarom as ons aanneem dat en , dan is .
Dan is die gemiddelde gradiënt
soos punt P nader beweeg aan punt Q, word kleiner. Dit beteken dat die gemiddelde gradiënt ook kleiner word. As die punt Q oorvleuel met die punt P, is en die gemiddelde gradiënt word gegee deur .
Ons sien nou dat ons die vergelyking kan skryf om die gemiddelde gradiënt op 'n effens anderse manier te bereken. As ons 'n kurwe het gedefineer deur , dan vir twee punte P en Q met P en Q , word die gemiddelde gradiënt tussen P en Q gegee deur :
Hierdie resultaat is belangrik om die gradiënt te bereken by 'n punt op 'n kurwe en dit sal in groter detail ondersoek word in Graad 12.

Notification Switch
Would you like to follow the 'Siyavula textbooks: wiskunde (graad 11)' conversation and receive update notifications?