| << Chapter < Page | Chapter >> Page > |
As a cautionary note, the results from the previous Concept Development Study make it clear that not every rate law is as simple as the one for the reaction of O 3 with Cl. We will return to this topic in a later section.
How is the effect of temperature change on the reaction rate reflected in the rate law equation? Recall that a rate law shows the dependence of the reaction rate on reactant concentrations, e.g. the rate of reaction of I 2 gas with H 2 as described in Equation (3) gas is given by the rate law in Equation (4).
H 2 (g) + I 2 (g) → 2HI(g)
Rate = k[H 2 ][I 2 ]
One possibility for the increase in the rate of this reaction when temperature is increased is that there is a slight dependence on temperature of the concentrations, since volumes do vary with temperature. However, this is insufficient to account for the dramatic changes in rate typically observed. Therefore, the temperature dependence of the reaction rate is primarily found in the rate constant, k . The rate constant of this reaction at each temperature can be found using the Method of Initial Rates, as discussed in the previous study, and we find in Table 1 that the rate constant increases dramatically as the temperature increases.
| T(K) | k (1/M∙sec) |
|---|---|
| 667 | 6.8×10 -3 |
| 675 | 9.87×10 -3 |
| 700 | 3.00×10 -2 |
| 725 | 8.43×10 -2 |
| 750 | 2.21×10 -1 |
| 775 | 5.46×10 -1 |
| 800 | 1.27 |
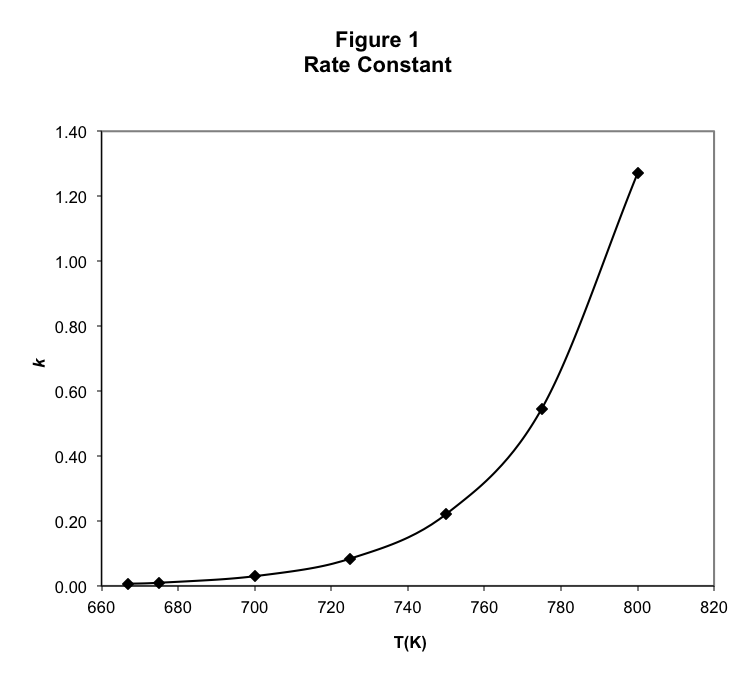
As shown in Figure 1, the rate constant appears to increase exponentially with temperature. After a little experimentation with the data, we find in Figure 2 that there is a simple linear relationship between ln( k ) and 1/T.

From Figure 2, we can see that the data in Table 1 fit the equation
ln (k) = a + b
where a and b are constant for this reaction. It turns out that, for our purposes, all reactions have rate constants that fit Equation (5), but with different constants a and b for each reaction. Figure 2 is referred to as an Arrhenius plot, after Svante Arrhenius.
It is not obvious why this equation should work for every chemical reaction. When we remember that the temperature is related to energy, it would seem that exothermic reactions and endothermic reactions should have different temperature dependence. Since they do not, this suggests that temperature increases and corresponding energy increases are not connected to the overall energy change of a reaction. This will lead us to a model to account for the temperature dependence of the rate constant. We will develop this further later in the next section.
Equation (5) is very convenient for describing the temperature dependence of a reaction. However, we would like some insight into why the temperature dependence should obey Equation (5), and in particular, into the meaning of the constants a and b in the equation.
As noted at the end of the last section, Equation (5) describes the rate constant temperature dependence regardless of whether the reaction is endothermic or exothermic. Therefore, whatever the energetic factor is that is required for the reaction to occur, it is not just that the reaction is endothermic. Exothermic reactions apparently require energy as well. It must be that all reactions, regardless of the overall change in energy, require energy to occur.

Notification Switch
Would you like to follow the 'Concept development studies in chemistry 2013' conversation and receive update notifications?