| << Chapter < Page | Chapter >> Page > |
Active transport mechanisms require the use of the cell’s energy, usually in the form of adenosine triphosphate (ATP). If a substance must move into the cell against its concentration gradient, that is, if the concentration of the substance inside the cell must be greater than its concentration in the extracellular fluid, the cell must use energy to move the substance. Some active transport mechanisms move small-molecular weight material, such as ions, through the membrane.
In addition to moving small ions and molecules through the membrane, cells also need to remove and take in larger molecules and particles. Some cells are even capable of engulfing entire unicellular microorganisms. You might have correctly hypothesized that the uptake and release of large particles by the cell requires energy. A large particle, however, cannot pass through the membrane, even with energy supplied by the cell.
We have discussed simple concentration gradients—differential concentrations of a substance across a space or a membrane—but in living systems, gradients are more complex. Because cells contain proteins, most of which are negatively charged, and because ions move into and out of cells, there is an electrical gradient, a difference of charge, across the plasma membrane. The interior of living cells is electrically negative with respect to the extracellular fluid in which they are bathed; at the same time, cells have higher concentrations of potassium (K + ) and lower concentrations of sodium (Na + ) than does the extracellular fluid. Thus, in a living cell, the concentration gradient and electrical gradient of Na + promotes diffusion of the ion into the cell, and the electrical gradient of Na + (a positive ion) tends to drive it inward to the negatively charged interior. The situation is more complex, however, for other elements such as potassium. The electrical gradient of K + promotes diffusion of the ion into the cell, but the concentration gradient of K + promotes diffusion out of the cell ( [link] ). The combined gradient that affects an ion is called its electrochemical gradient , and it is especially important to muscle and nerve cells.
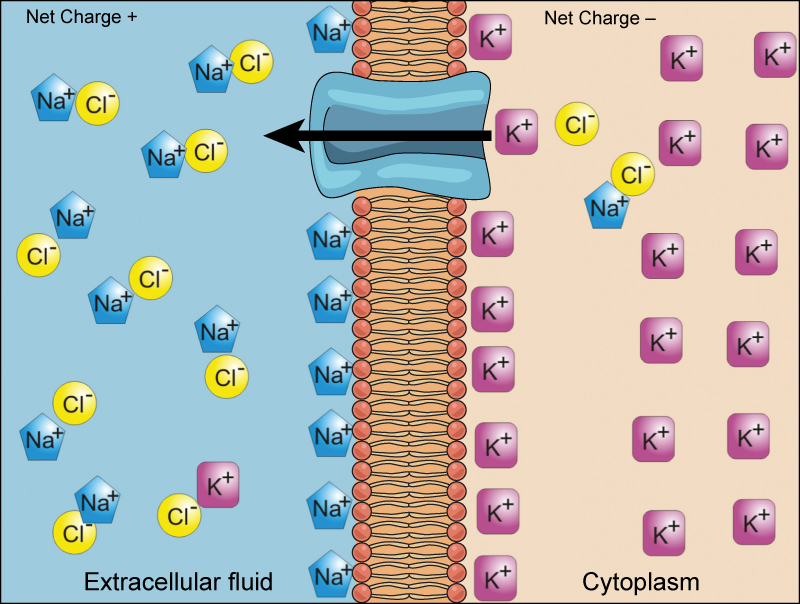
To move substances against a concentration or an electrochemical gradient, the cell must use energy. This energy is harvested from ATP that is generated through cellular metabolism. Active transport mechanisms, collectively called pumps or carrier proteins, work against electrochemical gradients. With the exception of ions, small substances constantly pass through plasma membranes. Active transport maintains concentrations of ions and other substances needed by living cells in the face of these passive changes. Much of a cell’s supply of metabolic energy may be spent maintaining these processes. Because active transport mechanisms depend on cellular metabolism for energy, they are sensitive to many metabolic poisons that interfere with the supply of ATP.

Notification Switch
Would you like to follow the 'Concepts of biology' conversation and receive update notifications?