| << Chapter < Page | Chapter >> Page > |
ACTIVITY 1:
To calculate the mechanical advantage of a hydraulic system
[LO 2.3]
An example of a simple hydraulic system is a hydraulic lift which is used to lift motor-cars. The system has a mechanical advantage of both power input and distance output.
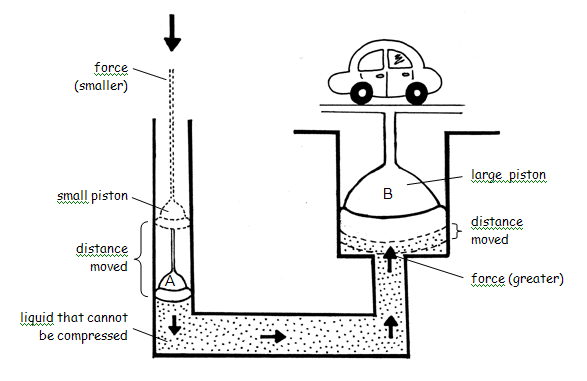
The system consists of two pistons of different sizes, connected by a reservoir that is filled with a hydraulic liquid such as oil or water.
Mechanical advantage – force multiplication:
A smaller input force on the small piston results in a greater output force on the large piston so that there is a mechanical advantage.
The input force is called the effort and the output force is called the load.
The advantage is made possible by two characteristics of liquids, namely that they cannot be compressed and that they distribute pressure equally.
This principle is called Pascal’s principle.
The pressure at piston A is equal to the pressure at piston B.
Pressure is calculated as force per area.
The following formula can be used to calculate the mechanical advantage:
Mechanical advantage – distance output:
In the syringes the piston with the large diameter will have a smaller distance output, and the piston with the small diameter will have a larger distance output. The relationship of distance output is determined by the mechanical force advantage.
Example:
The motor-car in the above example weighs 5 000 N. The small piston, A, has an area of 1cm². The small piston moves across a distance of 100 cm.

(a) Determine the input force. According to Pascal’s principle:
The area at cylinder B is 100 times bigger. Therefore the power at cylinder A is 100 times smaller.
(b) Determine the mechanical force advantage.
(c) Determine the distance that the large piston will move.
MA = 100. Therefore if the small piston moves 100 cm, the large piston will move 1 cm.
Test Your Knowledge

1.1 Calculate the amount of force, in Newton, that the little boy needs to make the Jack-in-the-Box weighing 100 g shoot out, when the area at cylinder A is 2cm² and the area at cylinder B is 1cm².
1.2 Calculate the mechanical advantage in question 1.1
1.3 Calculate the distance that piston A must move to make the Jack-in-the-Box shoot out 3 cm.
1.4 Would it be more advantageous to change around the two pistons, A and B?
2. You have to make a pair of hydraulic pliers, as indicated in the sketch. To enable you to do this, you are given two cylinders with pistons of 2 cm and 1 cm respectively. The maximum distance that the larger piston can move in the cylinder is 3 cm. A force of 1N is applied to move the moving jaws of the pliers over a distance of 3 cm and to clamp the jaws of the pliers.

2.1 Which of the two pistons are you going to place in position A for a minimum force input? Explain your answer.
2.2 How far will the piston at cylinder A move to clamp the jaws?
| LO 2 |
| TECHNOLOGICAL KNOWLEDGE AND UNDERSTANDINGThe learner will be able to understand and apply relevant technological knowledge ethically and responsibly. |
| We know this when the learner: |
| systems and control:2.3 demonstrates knowledge and understanding of interacting mechanical systems and sub-systems by practical analysis and represents them using systems diagrams:gear systemsbelt drive or pulley systems with more than one stage;mechanical control mechanisms (e.g. ratchet and pawl, cleats);pneumatic or hydraulic systems that use restrictorsone-way valves;systems where mechanical, electrical, or pneumatic or hydraulic systems are combined. |
ACTIVITY 1
1.1 FORCE = 2 N
1.2 MA=1/2
1.3 1,5 cm
1.4 No, the small piston/plunger will move the furthest and enable Jack to make the highest jump
2.1 The piston/plunger with a diameter of 1 cm
2.2 1,5 cm

Notification Switch
Would you like to follow the 'Technology grade 9' conversation and receive update notifications?