| << Chapter < Page | Chapter >> Page > |
Before you get started, take this readiness quiz.
How many quarters are pictured? One quarter plus quarters equals quarters.

Remember, quarters are really fractions of a dollar. Quarters are another way to say fourths. So the picture of the coins shows that
Let’s use fraction circles to model the same example,
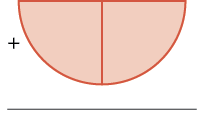
| Start with one piece. |
 |
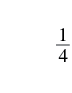 |
| Add two more pieces. |
 |
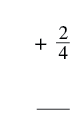 |
| The result is . |
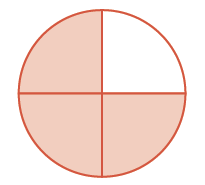 |
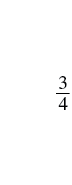 |
So again, we see that
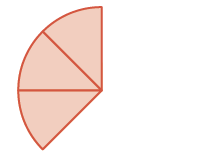
Use a model to find the sum
| Start with three pieces. |
 |
|
| Add two pieces. |
 |
|
| How many pieces are there? |
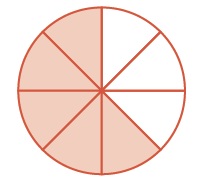 |
|
There are five pieces, or five-eighths. The model shows that
Use a model to find each sum. Show a diagram to illustrate your model.
Use a model to find each sum. Show a diagram to illustrate your model.

[link] shows that to add the same-size pieces—meaning that the fractions have the same denominator —we just add the number of pieces.
If are numbers where then
To add fractions with a common denominators, add the numerators and place the sum over the common denominator.
Find the sum:
| Add the numerators and place the sum over the common denominator. | |
| Simplify. |
Find the sum:
| Add the numerators and place the sum over the common denominator. |
Note that we cannot simplify this fraction any more. Since are not like terms, we cannot combine them.
Find the sum:
We will begin by rewriting the first fraction with the negative sign in the numerator.
| Rewrite the first fraction with the negative in the numerator. | |
| Add the numerators and place the sum over the common denominator. | |
| Simplify the numerator. | |
| Rewrite with negative sign in front of the fraction. |
Find the sum:
| Add the numerators and place the sum over the common denominator. | |
| Combine like terms. |
Find the sum:
| Add the numerators and place the sum over the common denominator. | |
| Add. | |
| Simplify the fraction. |
Subtracting two fractions with common denominators is much like adding fractions. Think of a pizza that was cut into slices. Suppose five pieces are eaten for dinner. This means that, after dinner, there are seven pieces (or of the pizza) left in the box. If Leonardo eats of these remaining pieces (or of the pizza), how much is left? There would be pieces left (or of the pizza).

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?