| << Chapter < Page | Chapter >> Page > |
1.1 Aantel
1.2 Haal elke keer 11 400 uit en tel res by
1.3 Hou 1000e, 100e, 10e en ene apart en tel op
1.4 Aantel: eers 10 000e, dan 1 000e, dan 100e, dan 10e en dan ene
1.5 Self-verduidelikend
1.6 Oordra-metode
2. Eie antwoord
3.2 Kort optelmetode sonder hulpsyfers
3.3
a) 83 320
b) 105 935
1. By Aktiwiteit 6 het julle jul eie tegnieke en strategieë gebruik om die probleme op te los. In jul terugvoering aan die klas het jul seker gesien dat daar talle maniere is waarop ons getalle bymekaar kan tel. Verdeel in ses groepe. Elke groep moet een van die volgende metodes bespreek en verduidelik hoe die antwoord bereken is.
HET JY GEWEET?
1.1 Ek bereken 11 468 + 23 957 so:
11 468 + 20 000 → 31 468 + 3 000 → 34 468 + 900
35 368 + 50 → 35 418 + 7 = 35 425
1.2 Ek verkies om die antwoord so te bereken:
11 468 + 23 957
= (11 400 + 11 400) + (68 + 12 557)
= (11 400 + 11 400 + 11 400) + (68 + 1 157)
= 34 200 + 1 225
= 35 425
1.3 Kyk mooi. Ek doen dit so:

1.4 My optelmetode lyk so:
11 468 + 23 957 =
10 000 + 20 000 → 30 000 + 1 000 + 3 000
34 000 + 400 + 900 → 35 300 + 60 + 50
35 410 + 8 + 7 = 35 425
1.5 Ek werk so:

1.6 Vir my is dit die maklikste om dit so neer te skryf:
11 468 + 23 957:

2. Watter metode is vir jou die maklikste? Motiveer jou antwoord.
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
3. Werk nou saam met ‘n maat en kyk goed na die volgende metode:
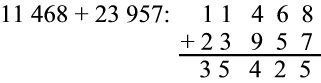
3.2 Verduidelik die metode vir ‘n ander maat.
3.3 Gebruik nou hierdie metode en bereken die som van die volgende:
a) 35 691 + 47 629
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
b) 82 179 + 23 756
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
Kom ons kyk hoe het jy gevaar.
Merk die toepaslike blokkie:
| Ek verstaan | al die metodes. | die meeste van die metodes. | **net een of twee van die metodes. |
** Vra jou groeplede / opvoeder om dit weer vir jou te verduidelik.
Werk in groepe van vier. Kan julle aan nog enige ANDER metodes dink om die som van 11 468 + 23 957 te bereken?
Leeruitkomste 1: Die leerder is in staat om getalle en die verwantskappe daarvan te herken, te beskryf en voor te stel, en om tydens probleemoplossing bevoeg en met selfvertroue te tel, te skat, te bereken en te kontroleer.
Assesseringstandaard 1.11: Dit is duidelik wanneer die leerder ‘n verskeidenheid strategieë gebruik om oplossings te kontroleer en die redelikheid van oplossings te beoordeel.
Leeruitkomste 2: Die leerder is in staat om patrone en verwantskappe te herken, te beskryf en voor te stel en probleme op te los deur algebraïese taal en vaardighede te gebruik.
Assesseringstandaard 2.6: Dit is duidelik wanneer die leerder bepaal, deur bespreking en vergelyking, die ekwivalensie van verskillende beskrywings van dieselfde verwantskap of reël wat soos volg voorgestel word:
2.6.1 woordeliks;
2.6.2 in vloeidiagramme;
2.6.3 met getalsinne.

Notification Switch
Would you like to follow the 'Wiskunde graad 5' conversation and receive update notifications?