| << Chapter < Page | Chapter >> Page > |
INTRODUCTION
The Grade 1 educator needs to determine whether the learners have attended a pre-primary class or not. For the learners who have not attended a pre-primary, Modules 1 and 2 may have to be adapted to include more activities so as to reinforce the vocabulary and concepts in these modules. For the learners who have attended pre-primary schools, Modules 1 and 2 will serve as revision exercises giving the educator a clear picture as to what they know.
TIME SCHEDULE
Two modules have been designed for each term. The educator may however find that the fast workers will complete the modules in less time than the slower workers. The educator should feel free to extend the number range for the learners who are ready for it. The minimum requirements for the slow learners are Modules 1 to 7.
Critical and developmental outcomes:
The learners must be able to:
1. identify and solve problems and make decisions using critical and creative thinking;
2. work effectively with others as members of a team, group, organisation and community;
3. organise and manage themselves and their activities responsibly and effectively;
4. collect, analyse, organise and critically evaluate information;
5. communicate effectively using visual, symbolic and/or language skills in various modes;
6. use science and technology effectively and critically, showing responsibility towards the environment and the health of others;
7. demonstrate an understanding of the world as a set of related systems by recognising that problem-solving contexts do not exist in isolation;
8. reflect on and explore a variety of strategies to learn more effectively;
9. participate as responsible citizens in the life of local, national, and global communities;
10. be culturally and aesthetically sensitive across a range of social contexts;
11. explore education and career opportunities; and
12. develop entrepreneurial opportunities.
The three bears help the learners to understand:
Five little bears
heard a lion roar
one went up too close
and then there were four.
Four little bears
climbed up a tree
one came tumbling down
and there were three.
Three little bears
tried to cook a stew
one cut his finger
and then there were two.
Two little bears
were sitting in the sun
one stayed there far too long
and then there was one.
One little bear
went for a run
he didn’t turn back again
and now there are none.
R. Louw
| LO 1.2 |


| LO 1.1 | LO 1.3 | LO 1.4 |


| LO 1.3 |


| LO 1.2 | LO 3.1 | LO 5.2 | LO 5.3 |
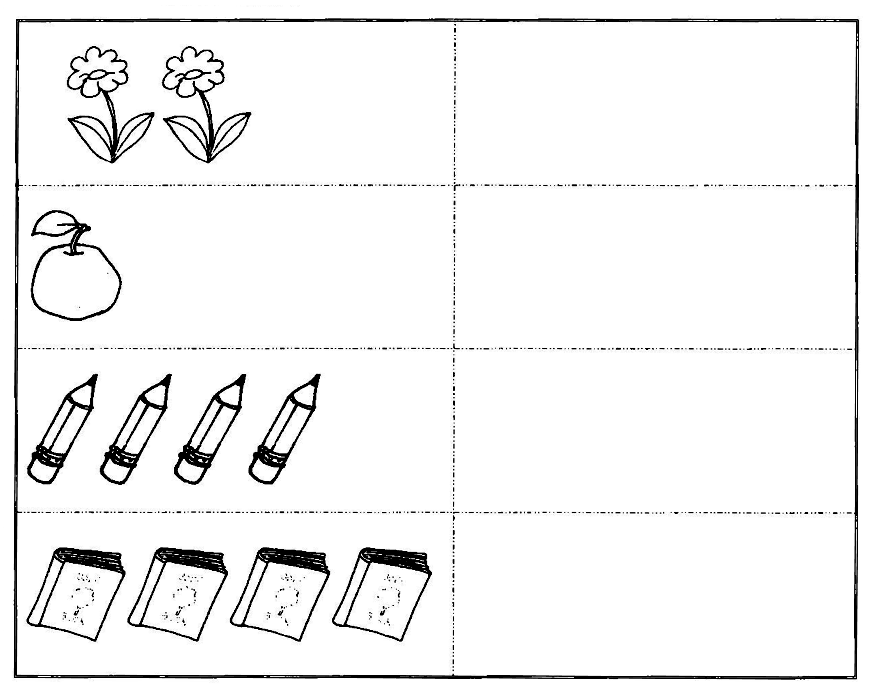

| LO 1.3 | LO 1.9 |


| LO 1.1 | LO 1.3 |

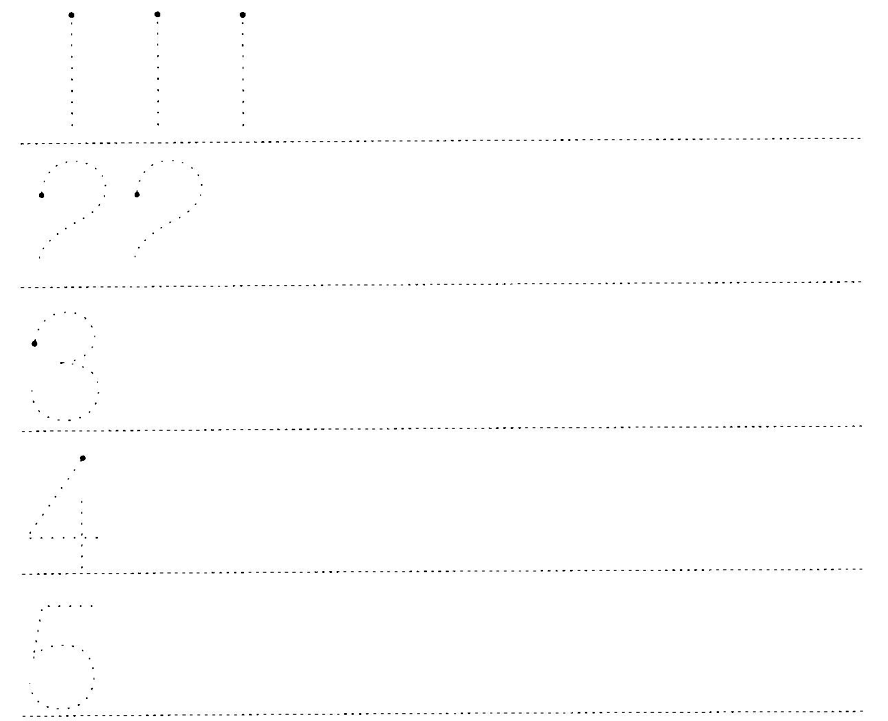
| LO 1.3 |
| 2 | 1 | 3 | 4 | 5 |
| 1 | ___ | ___ | ___ | ___ |
| 4 | 3 | 2 | 1 | 5 |
| 1 | ___ | ___ | ___ | ___ |
| 3 | 2 | 5 | 1 | 4 |
| ___ | ___ | ___ | ___ | ___ |

| LO 1.1 | LO 1.4 |

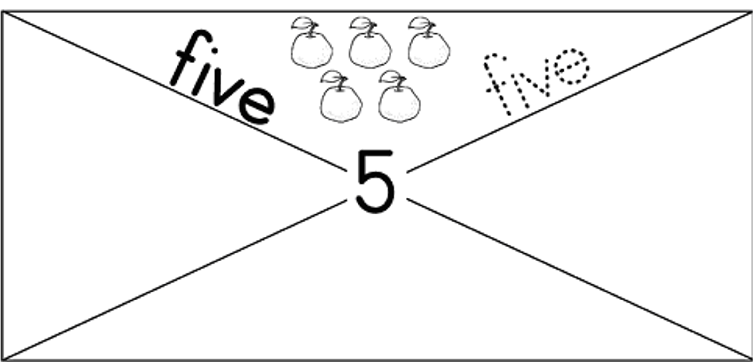
| LO 1.3 | LO 1.6 |
Learning Outcome 1: NUMBERS, OPERATIONS AND RELATIONSHIPS: The learner will be able to recognise, describe and represent numbers and their relationships, and to count, estimate, calculate and check with competence and confidence in solving problems.
Assessment Standard 1.1: We know this when the learner counts to at least 34 everyday objects reliably;
Assessment Standard 1.2: We know this when the learner counts forwards and backwards;
Assessment Standard 1.3: We know this when the learner knows and reads number symbols from 1 to at least 100 and writes number names from 1 to at least 34;
Assessment Standard 1.4: We know this when the learner orders, describes and compares whole numbers to at least 2-digit numbers;
Assessment Standard 1.6: We know this when the learner solves and explains solutions to practical problems that involve equal sharing and grouping with whole numbers to at least 34 and with solutions that include remainders;
Assessment Standard 1.9: We know this when the learner uses techniques
Learning Outcome 3: SPACE AND SHAPE (GEOMETRY): The learner will be able to describe and represent characteristics and relationships between two-dimensional shapes and three-dimensional objects in a variety of orientations and positions.
Assessment Standard 3.1: We know this when the learner recognises, identifies and names two-dimensional shapes and three-dimensional objects in the classroom and in pictures;
Learning Outcome 5: DATA HANDLING : The learner will be able to collect, summarise, display and critically analyse data in order to draw conclusions and make predictions, and to interpret and determine chance variation.
Assessment Standard 5.2: We know this when the learner sorts physical objects according to one attribute chosen for a reason (e.g. ‘Sort crayons into colours’);
Assessment Standard 5.3: We know this when the learner gives reasons for collections being grouped in particular ways.

Notification Switch
Would you like to follow the 'Mathematics grade 1' conversation and receive update notifications?