-
Home
- Calculus volume 3
- Vector calculus
- The divergence theorem
Key concepts
- The divergence theorem relates a surface integral across closed surface
S to a triple integral over the solid enclosed by
S . The divergence theorem is a higher dimensional version of the flux form of Green’s theorem, and is therefore a higher dimensional version of the Fundamental Theorem of Calculus.
- The divergence theorem can be used to transform a difficult flux integral into an easier triple integral and vice versa.
- The divergence theorem can be used to derive Gauss’ law, a fundamental law in electrostatics.
Key equations
-
Divergence theorem
For the following exercises, use a computer algebraic system (CAS) and the divergence theorem to evaluate surface integral
for the given choice of
F and the boundary surface
S. For each closed surface, assume
N is the outward unit normal vector.
[T]
S is the surface of hemisphere
together with disk
in the
xy -plane.
Got questions? Get instant answers now!
[T]
S is the surface bounded above by sphere
and below by cone
in spherical coordinates. (Think of
S as the surface of an “ice cream cone.”)
Got questions? Get instant answers now!
[T]
S is the surface bounded by cylinder
and planes
Got questions? Get instant answers now!
[T] Surface integral
where
S is the solid bounded by paraboloid
and plane
and
Got questions? Get instant answers now!
Use the divergence theorem to calculate surface integral
where
and
S is upper hemisphere
oriented upward.
Got questions? Get instant answers now!
Use the divergence theorem to calculate surface integral
where
and S is the surface bounded by cylinder
and planes
and
Got questions? Get instant answers now!
Use the divergence theorem to calculate surface integral
when
and
S is the surface of the box with vertices
Got questions? Get instant answers now!
Use the divergence theorem to calculate surface integral
when
and
S is a part of paraboloid
that lies above plane
and is oriented upward.
Got questions? Get instant answers now!
[T] Use a CAS and the divergence theorem to calculate flux
where
and
S is a sphere with center (0, 0) and radius 2.
Got questions? Get instant answers now!
Use the divergence theorem to compute the value of flux integral
where
and
S is the area of the region bounded by
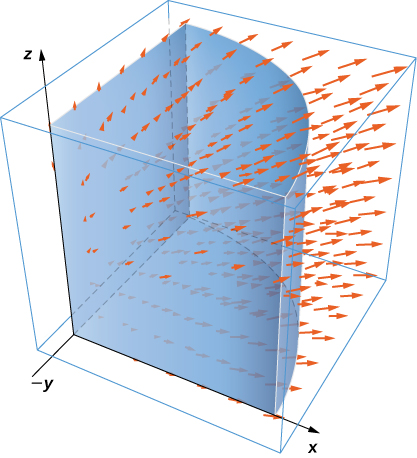
Got questions? Get instant answers now!
Use the divergence theorem to compute flux integral
where
and
S consists of the union of paraboloid
and disk
oriented outward. What is the flux through just the paraboloid?
Got questions? Get instant answers now!
Source:
OpenStax, Calculus volume 3. OpenStax CNX. Feb 05, 2016 Download for free at http://legacy.cnx.org/content/col11966/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

