-
Home
- Calculus volume 3
- Vector-valued functions
- Calculus of vector-valued
Key concepts
- To calculate the derivative of a vector-valued function, calculate the derivatives of the component functions, then put them back into a new vector-valued function.
- Many of the properties of differentiation from the
Introduction to Derivatives also apply to vector-valued functions.
- The derivative of a vector-valued function
is also a tangent vector to the curve. The unit tangent vector
is calculated by dividing the derivative of a vector-valued function by its magnitude.
- The antiderivative of a vector-valued function is found by finding the antiderivatives of the component functions, then putting them back together in a vector-valued function.
- The definite integral of a vector-valued function is found by finding the definite integrals of the component functions, then putting them back together in a vector-valued function.
Key equations
-
Derivative of a vector-valued function
-
Principal unit tangent vector
-
Indefinite integral of a vector-valued function
-
Definite integral of a vector-valued function
Compute the derivatives of the vector-valued functions.
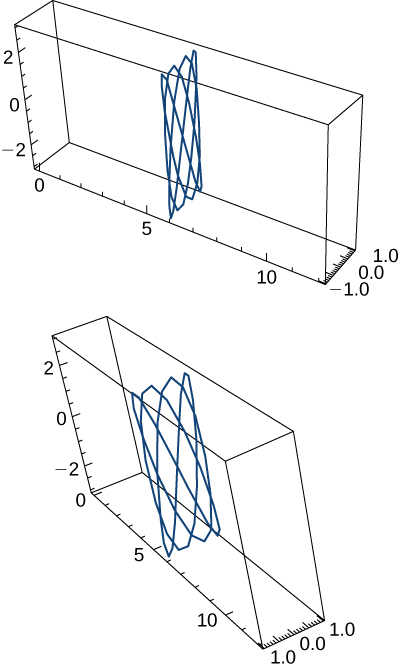
A sketch of the graph is shown here. Notice the varying periodic nature of the graph.
Got questions? Get instant answers now!
For the following problems, find a tangent vector at the indicated value of
t .
Find the unit tangent vector for the following parameterized curves.
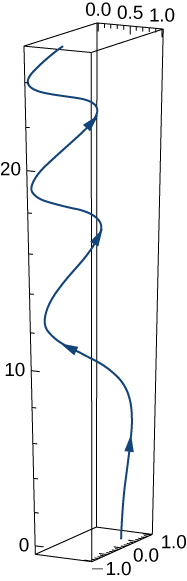
Let
and
Here is the graph of the function:
Find the following.
The acceleration function, initial velocity, and initial position of a particle are
Find
Got questions? Get instant answers now!
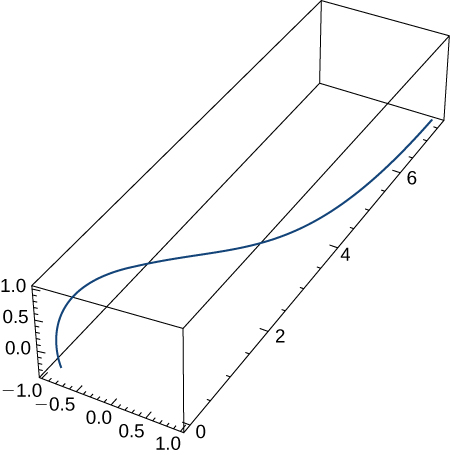
The position vector of a particle is
- Graph the position function and display a view of the graph that illustrates the asymptotic behavior of the function.
- Find the velocity as
t approaches but is not equal to
(if it exists).
-
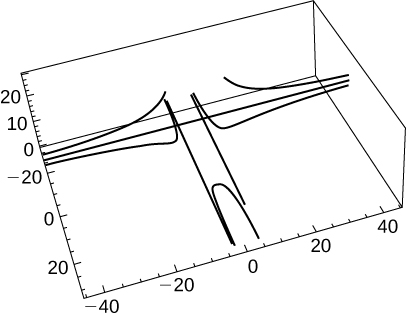
- Undefined or infinite
Got questions? Get instant answers now!
Find the velocity and the speed of a particle with the position function
The speed of a particle is the magnitude of the velocity and is represented by
Got questions? Get instant answers now!
Source:
OpenStax, Calculus volume 3. OpenStax CNX. Feb 05, 2016 Download for free at http://legacy.cnx.org/content/col11966/1.2
Google Play and the Google Play logo are trademarks of Google Inc.