| << Chapter < Page | Chapter >> Page > |
When the endpoints of a line segment are known, we can find the point midway between them. This point is known as the midpoint and the formula is known as the midpoint formula . Given the endpoints of a line segment, and the midpoint formula states how to find the coordinates of the midpoint
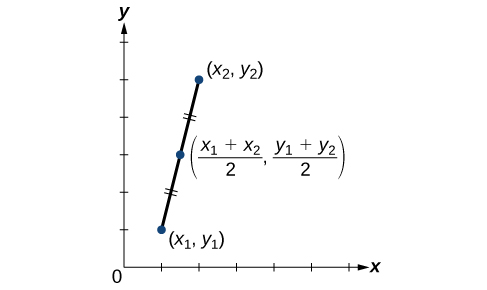
A graphical view of a midpoint is shown in [link] . Notice that the line segments on either side of the midpoint are congruent.
Find the midpoint of the line segment with the endpoints and
Use the formula to find the midpoint of the line segment.
The diameter of a circle has endpoints and Find the center of the circle.
The center of a circle is the center, or midpoint, of its diameter. Thus, the midpoint formula will yield the center point.
Access these online resources for additional instruction and practice with the Cartesian coordinate system.
Is it possible for a point plotted in the Cartesian coordinate system to not lie in one of the four quadrants? Explain.
Answers may vary. Yes. It is possible for a point to be on the x -axis or on the y -axis and therefore is considered to NOT be in one of the quadrants.
Describe the process for finding the x- intercept and the y -intercept of a graph algebraically.
Describe in your own words what the y -intercept of a graph is.
The y -intercept is the point where the graph crosses the y -axis.
When using the distance formula explain the correct order of operations that are to be performed to obtain the correct answer.
For each of the following exercises, find the x -intercept and the y -intercept without graphing. Write the coordinates of each intercept.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?