-
Home
- Calculus volume 1
- Integration
- The fundamental theorem of
Key concepts
- The Mean Value Theorem for Integrals states that for a continuous function over a closed interval, there is a value
c such that
equals the average value of the function. See
[link] .
- The Fundamental Theorem of Calculus, Part 1 shows the relationship between the derivative and the integral. See
[link] .
- The Fundamental Theorem of Calculus, Part 2 is a formula for evaluating a definite integral in terms of an antiderivative of its integrand. The total area under a curve can be found using this formula. See
[link] .
Key equations
-
Mean Value Theorem for Integrals
If
is continuous over an interval
then there is at least one point
such that
-
Fundamental Theorem of Calculus Part 1
If
is continuous over an interval
and the function
is defined by
then
-
Fundamental Theorem of Calculus Part 2
If
f is continuous over the interval
and
is any antiderivative of
then
Consider two athletes running at variable speeds
and
The runners start and finish a race at exactly the same time. Explain why the two runners must be going the same speed at some point.
Got questions? Get instant answers now!
Two mountain climbers start their climb at base camp, taking two different routes, one steeper than the other, and arrive at the peak at exactly the same time. Is it necessarily true that, at some point, both climbers increased in altitude at the same rate?
Yes. It is implied by the Mean Value Theorem for Integrals.
Got questions? Get instant answers now!
To get on a certain toll road a driver has to take a card that lists the mile entrance point. The card also has a timestamp. When going to pay the toll at the exit, the driver is surprised to receive a speeding ticket along with the toll. Explain how this can happen.
Got questions? Get instant answers now!
Set
Find
and the average value of
over
average value of
over
is
Got questions? Get instant answers now!
In the following exercises, use the Fundamental Theorem of Calculus, Part 1, to find each derivative.
The graph of
where
f is a piecewise constant function, is shown here.
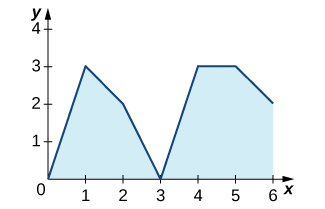
- Over which intervals is
f positive? Over which intervals is it negative? Over which intervals, if any, is it equal to zero?
- What are the maximum and minimum values of
f ?
- What is the average value of
f ?
Got questions? Get instant answers now!
The graph of
where
f is a piecewise constant function, is shown here.
![A graph of a function with linear segments that goes through the points (0, 0), (1, -1), (2, 1), (3, 1), (4, -2), (5, -2), and (6, 0). The area over the function but under the x axis over the interval [0, 1.5] and [3.25, 6] is shaded. The area under the function but over the x axis over the interval [1.5, 3.25] is shaded.](/ocw/mirror/col11964/m53632/CNX_Calc_Figure_05_03_203.jpg)
- Over which intervals is
f positive? Over which intervals is it negative? Over which intervals, if any, is it equal to zero?
- What are the maximum and minimum values of
f ?
- What is the average value of
f ?
a.
f is positive over
and
negative over
and
and zero over
and
b. The maximum value is 2 and the minimum is −3. c. The average value is 0.
Got questions? Get instant answers now!
The graph of
where
ℓ is a piecewise linear function, is shown here.
![A graph of a function which goes through the points (0, 0), (1, -1), (2, 1), (3, 3), (4, 3.5), (5, 4), and (6, 2). The area over the function and under the x axis over [0, 1.8] is shaded, and the area under the function and over the x axis is shaded.](/ocw/mirror/col11964/m53632/CNX_Calc_Figure_05_03_204.jpg)
- Over which intervals is
ℓ positive? Over which intervals is it negative? Over which, if any, is it zero?
- Over which intervals is
ℓ increasing? Over which is it decreasing? Over which, if any, is it constant?
- What is the average value of
ℓ ?
Got questions? Get instant answers now!
Source:
OpenStax, Calculus volume 1. OpenStax CNX. Feb 05, 2016 Download for free at http://cnx.org/content/col11964/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

![A graph of a function with linear segments that goes through the points (0, 0), (1, -1), (2, 1), (3, 1), (4, -2), (5, -2), and (6, 0). The area over the function but under the x axis over the interval [0, 1.5] and [3.25, 6] is shaded. The area under the function but over the x axis over the interval [1.5, 3.25] is shaded.](/ocw/mirror/col11964/m53632/CNX_Calc_Figure_05_03_203.jpg)
![A graph of a function which goes through the points (0, 0), (1, -1), (2, 1), (3, 3), (4, 3.5), (5, 4), and (6, 2). The area over the function and under the x axis over [0, 1.8] is shaded, and the area under the function and over the x axis is shaded.](/ocw/mirror/col11964/m53632/CNX_Calc_Figure_05_03_204.jpg)
