| << Chapter < Page | Chapter >> Page > |
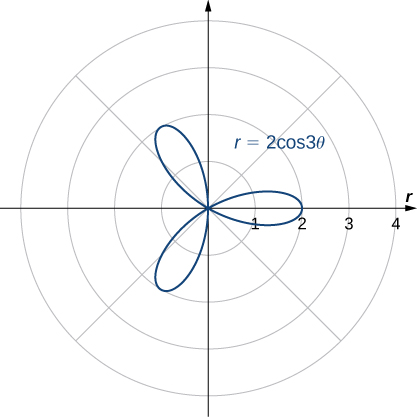
Determine the symmetry of the graph determined by the equation and create a graph.
Symmetric with respect to the polar axis.
In the following exercises, plot the point whose polar coordinates are given by first constructing the angle and then marking off the distance r along the ray.
For the following exercises, consider the polar graph below. Give two sets of polar coordinates for each point.
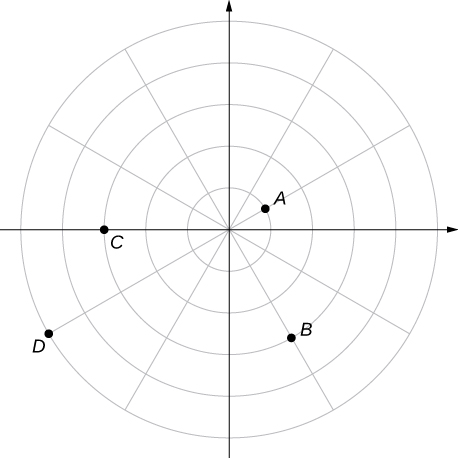
Coordinates of point A .
Coordinates of point C .
For the following exercises, the rectangular coordinates of a point are given. Find two sets of polar coordinates for the point in Round to three decimal places.
For the following exercises, find rectangular coordinates for the given point in polar coordinates.
For the following exercises, determine whether the graphs of the polar equation are symmetric with respect to the -axis, the -axis, or the origin.
For the following exercises, describe the graph of each polar equation. Confirm each description by converting into a rectangular equation.
For the following exercises, convert the rectangular equation to polar form and sketch its graph.
For the following exercises, convert the rectangular equation to polar form and sketch its graph.
For the following exercises, convert the polar equation to rectangular form and sketch its graph.
For the following exercises, sketch a graph of the polar equation and identify any symmetry.
[T] The graph of is called a strophoid. Use a graphing utility to sketch the graph, and, from the graph, determine the asymptote.
[T] Use a graphing utility to graph
[T] Use technology to plot (use the interval
[T] Use a graphing utility to plot for
[T] There is a curve known as the “ Black Hole .” Use technology to plot for
[T] Use the results of the preceding two problems to explore the graphs of and for
Answers vary. One possibility is the spiral lines become closer together and the total number of spirals increases.

Notification Switch
Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?