1. Home
  2. Calculus volume 2
  3. Introduction to differential
  4. Direction fields and numerical

4.2 Direction fields and numerical methods  (Page 5/14)

<< Chapter < Page
  Calculus volume 2     Page 5 / 14
Chapter >> Page >

Typically h is a small value, say 0.1 or 0.05 . The smaller the value of h , the more calculations are needed. The higher the value of h , the fewer calculations are needed. However, the tradeoff results in a lower degree of accuracy for larger step size, as illustrated in [link] .

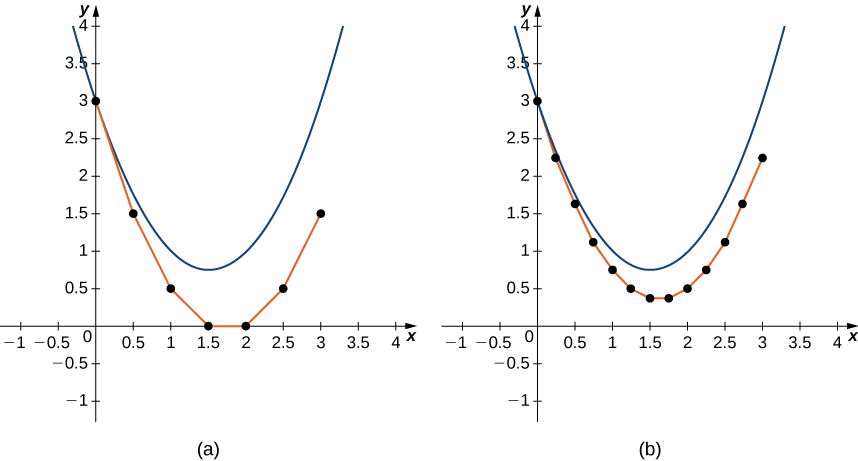
Two graphs of the same parabola, y = x ^ 2 – 3 x + 3. The first shows Euler’s method for the given initial-value problem with a step size of h = 0.05, and the second shows Euler’s method with a step size of h = 0.25. The first then has the points (0, 3), (.5, 1.5), (1, 0.5), (1.5, 0), (2, 0), (2.5, 0.5), and (3, 1.5) plotted with line segments connecting them. The second has the points (0, 3), (0.25, 2.25), (0.5, 1.625), (0.75, 1.125), (1, 0.75), (1.25, 0.5), (1.5, 0.375), (2, 0.5), (2.25, 0.75), (2.5, 1.125), (2.75, 1.625), and (3, 2.25) plotted with line segments connecting them.
Euler’s method for the initial-value problem y ′ = 2 x − 3 , y ( 0 ) = 3 with (a) a step size of h = 0.5 ; and (b) a step size of h = 0.25 .

Using euler’s method

Consider the initial-value problem

y ′ = 3 x 2 − y 2 + 1 , y ( 0 ) = 2 .

Use Euler’s method with a step size of 0.1 to generate a table of values for the solution for values of x between 0 and 1 .

We are given h = 0.1 and f ( x , y ) = 3 x 2 − y 2 + 1 . Furthermore, the initial condition y ( 0 ) = 2 gives x 0 = 0 and y 0 = 2 . Using [link] with n = 0 , we can generate [link] .

Using euler’s method to approximate solutions to a differential equation
n x n y n = y n − 1 + h f ( x n − 1 , y n − 1 )
0 0 2
1 0.1 y 1 = y 0 + h f ( x 0 , y 0 ) = 1.7
2 0.2 y 2 = y 1 + h f ( x 1 , y 1 ) = 1.514
3 0.3 y 3 = y 2 + h f ( x 2 , y 2 ) = 1.3968
4 0.4 y 4 = y 3 + h f ( x 3 , y 3 ) = 1.3287
5 0.5 y 5 = y 4 + h f ( x 4 , y 4 ) = 1.3001
6 0.6 y 6 = y 5 + h f ( x 5 , y 5 ) = 1.3061
7 0.7 y 7 = y 6 + h f ( x 6 , y 6 ) = 1.3435
8 0.8 y 8 = y 7 + h f ( x 7 , y 7 ) = 1.4100
9 0.9 y 9 = y 8 + h f ( x 8 , y 8 ) = 1.5032
10 1.0 y 10 = y 9 + h f ( x 9 , y 9 ) = 1.6202

With ten calculations, we are able to approximate the values of the solution to the initial-value problem for values of x between 0 and 1 .

Got questions? Get instant answers now!
Got questions? Get instant answers now!

Go to this website for more information on Euler’s method.

Consider the initial-value problem

y ′ = x 3 + y 2 , y ( 1 ) = −2 .

Using a step size of 0.1 , generate a table with approximate values for the solution to the initial-value problem for values of x between 1 and 2 .

n x n y n = y n − 1 + h f ( x n − 1 , y n − 1 )
0 1 −2
1 1.1 y 1 = y 0 + h f ( x 0 , y 0 ) = −1.5
2 1.2 y 2 = y 1 + h f ( x 1 , y 1 ) = −1.1419
3 1.3 y 3 = y 2 + h f ( x 2 , y 2 ) = −0.8387
4 1.4 y 4 = y 3 + h f ( x 3 , y 3 ) = −0.5487
5 1.5 y 5 = y 4 + h f ( x 4 , y 4 ) = −0.2442
6 1.6 y 6 = y 5 + h f ( x 5 , y 5 ) = 0.0993
7 1.7 y 7 = y 6 + h f ( x 6 , y 6 ) = 0.5099
8 1.8 y 8 = y 7 + h f ( x 7 , y 7 ) = 1.0272
9 1.9 y 9 = y 8 + h f ( x 8 , y 8 ) = 1.7159
10 2 y 10 = y 9 + h f ( x 9 , y 9 ) = 2.6962
Got questions? Get instant answers now!

Visit this website for a practical application of the material in this section.

Key concepts

  • A direction field is a mathematical object used to graphically represent solutions to a first-order differential equation.
  • Euler’s Method is a numerical technique that can be used to approximate solutions to a differential equation.

Key equations

  • Euler’s Method
    x n = x 0 + n h y n = y n − 1 + h f ( x n − 1 , y n − 1 ) , where h is the step size

For the following problems, use the direction field below from the differential equation y ′ = −2 y . Sketch the graph of the solution for the given initial conditions.
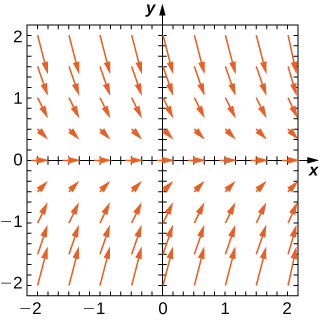
A direction field with horizontal arrows pointing to the right at 0. The arrows above the x axis point down and to the right. The further away from the x axis, the steeper the arrows are, and the closer to the x axis, the flatter the arrows are. Likewise, the arrows below the x axis point up and to the right. The further away from the x axis, the steeper the arrows are, and the closer to the x axis, the flatter the arrows are.

y ( 0 ) = 1

Got questions? Get instant answers now!

y ( 0 ) = 0


A graph of the given direction field with a flat line drawn on the axis. The arrows point up for y < 0 and down for y > 0. The closer they are to the x axis, the more horizontal the arrows are, and the further away they are, the more vertical they become.

Got questions? Get instant answers now!

y ( 0 ) = −1

Got questions? Get instant answers now!

Are there any equilibria? What are their stabilities?

y = 0 is a stable equilibrium

Got questions? Get instant answers now!

For the following problems, use the direction field below from the differential equation y ′ = y 2 − 2 y . Sketch the graph of the solution for the given initial conditions.
A direction field with horizontal arrows at y = 0 and y = 2. The arrows point up for y > 2 and for y < 0. The arrows point down for 0 < y < 2. The closer the arrows are to these lines, the more horizontal they are, and the further away, the more vertical the arrows are.

y ( 0 ) = 3

Got questions? Get instant answers now!

y ( 0 ) = 1


A direction field with horizontal arrows at y = 0 and y = 2. The arrows point up for y > 2 and for y < 0. The arrows point down for 0 < y < 2. The closer the arrows are to these lines, the more horizontal they are, and the further away, the more vertical the arrows are. A solution is sketched that follows y = 2 in quadrant two, goes through (0, 1), and then follows the x axis.

Got questions? Get instant answers now!

y ( 0 ) = −1

Got questions? Get instant answers now!

Are there any equilibria? What are their stabilities?

y = 0 is a stable equilibrium and y = 2 is unstable

Got questions? Get instant answers now!

Draw the direction field for the following differential equations, then solve the differential equation. Draw your solution on top of the direction field. Does your solution follow along the arrows on your direction field?

y ′ = t 3

Got questions? Get instant answers now!

y ′ = e t


A direction field over the four quadrants. As t goes from 0 to infinity, the arrows become more and more vertical after being horizontal closer to x = 0.

Got questions? Get instant answers now!

d y d x = x 2 cos x

Got questions? Get instant answers now!

d y d t = t e t


A direction field over [-2, 2] in the x and y axes. The arrows point slightly down and to the right over [-2, 0] and gradually become vertical over [0, 2].

Got questions? Get instant answers now!

d x d t = cosh ( t )

Got questions? Get instant answers now!

Draw the directional field for the following differential equations. What can you say about the behavior of the solution? Are there equilibria? What stability do these equilibria have?
<< Chapter < Page Page > Chapter >>
Practice Key Terms 8

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Calculus volume 2. OpenStax CNX. Feb 05, 2016 Download for free at http://cnx.org/content/col11965/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 2' conversation and receive update notifications?

Ask