| << Chapter < Page | Chapter >> Page > |
This chapter is about how things move in a straight line or more scientifically how things move in one dimension . This is useful for learning how to describe the movement of cars along a straight road or of trains along straight railway tracks. If you want to understand how any object moves, for example a car on the freeway, a soccer ball being kicked towards the goal or your dog chasing the neighbour's cat, then you have to understand three basic ideas about what it means when something is moving . These three ideas describe different parts of exactly how an object moves. They are:
You will also learn how to use position, displacement, speed, velocity and acceleration to describe the motion of simple objects. You will learn how to read and draw graphs that summarise the motion of a moving object. You will also learn about the equations that can be used to describe motion and how to apply these equations to objects moving in one dimension.
The most important idea when studying motion, is you have to know where you are. The word position describes your location (where you are). However, saying that you are here is meaningless, and you have to specify your position relative to a known reference point. For example, if you are 2 m from the doorway, inside your classroom then your reference point is the doorway. This defines your position inside the classroom. Notice that you need a reference point (the doorway) and a direction (inside) to define your location.
A frame of reference is a reference point combined with a set of directions.
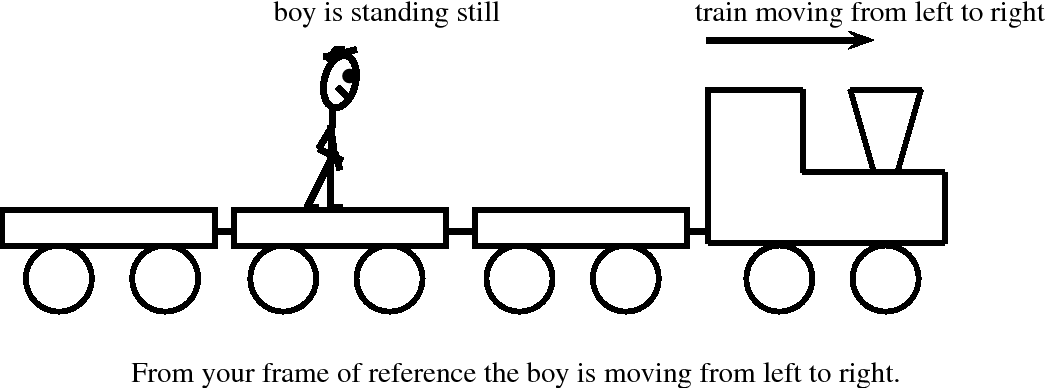
A frame of reference is similar to the idea of a reference point. A frame of reference is defined as a reference point combined with a set of directions. For example, a boy is standing still inside a train as it pulls out of a station. You are standing on the platform watching the train move from left to right. To you it looks as if the boy is moving from left to right, because relative to where you are standing (the platform), he is moving. According to the boy, and his frame of reference (the train), he is not moving.
A frame of reference must have an origin (where you are standing on the platform) and at least a positive direction. The train was moving from left to right, making to your right positive and to your left negative. If someone else was looking at the same boy, his frame of reference will be different. For example, if he was standing on the other side of the platform, the boy will be moving from right to left.
Another great example of frames of reference is a car overtaking another car on a road. Think about sitting in a taxi passing a car. If you sit in the taxi it is your origin and the direction it is moving in will be the positive direction. You will see the car slowly move further behind you (in the negative direction). The very important thing is that the driver of the car has their own reference frame in which things look different. In the driver's reference frame the taxi is moving ahead. In one case someone is falling behind, but in the other case someone is moving ahead. This is just a matter of perspective (from which reference frame you choose to view the situation).
For this chapter, we will only use frames of reference in the -direction. Frames of reference will be covered in more detail in Grade 12.

Position is a measurement of a location, with reference to an origin.
A position is a measurement of a location, with reference to an origin. Positions can therefore be negative or positive. The symbol is used to indicate position. has units of length for example cm, m or km. [link] shows the position of a school. Depending on what reference point we choose, we can say that the school is from Joan's house (with Joan's house as the reference point or origin) or from Joel's house (with Joel's house as the reference point or origin).

The shop is also from Joan's house, but in the opposite direction as the school. When we choose a reference point, we have a positive direction and a negative direction. If we choose the direction towards the school as positive, then the direction towards the shop is negative. A negative direction is always opposite to the direction chosen as positive.

Divide into groups of 5 for this activity. On a straight line, choose a reference point. Since position can have both positive and negative values, discuss the advantages and disadvantages of choosing
This reference point can also be called “the origin".




Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 physical science [caps]' conversation and receive update notifications?