| << Chapter < Page | Chapter >> Page > |
Hopefully you are familiar with the notion of the eigenvectors of a "matrix system," if not they do a quick review of eigen-stuff . We can develop the same ideas for LTI systems acting on signals. A linear time invariant (LTI) system operating on a continuous input to produce continuous time output

is mathematically analogous to an x matrix operating on a vector to produce another vector (seeMatrices and LTI Systemsfor an overview).

Just as an
eigenvector of
is a
such that
,
,

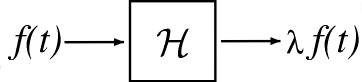
Eigenfunctions are the simplest possible signals for to operate on: to calculate the output, we simply multiply the input by a complex number .
The class of LTI systems has a set of eigenfunctions in common: the complex exponentials , are eigenfunctions for all LTI systems.

We can prove [link] by expressing the output as a convolution of the input and the impulse response of :

Since the action of an LTI operator on its eigenfunctions is easy to calculate and interpret, it is convenient to represent an arbitrary signal as a linear combination of complex exponentials. The Fourier series gives us this representation for periodic continuous timesignals, while the (slightly more complicated) Fourier transform lets us expand arbitrary continuous time signals.

Notification Switch
Would you like to follow the 'Signals and systems' conversation and receive update notifications?