| << Chapter < Page | Chapter >> Page > |

Finding the maximum cut of a graph is a difficult to compute problem in combinatorial optimization with several applications in the world of engineering and physics. This research develops and evaluates an exact branch and bound algorithm for the maximum cut of unweighted graphs that is designed for improved performance on sparse graphs.
The module provides a general overview of the problem along with necessary mathematical background in "The Maxcut Problem" and a brief note on various approaches to the problem in "Several Algorithms" . "A New Algorithm" describes a new algorithm for finding maximum cuts. Results of empirical performance evaluation appear in "Empirical Testing" , which "Conclusion" further discusses.
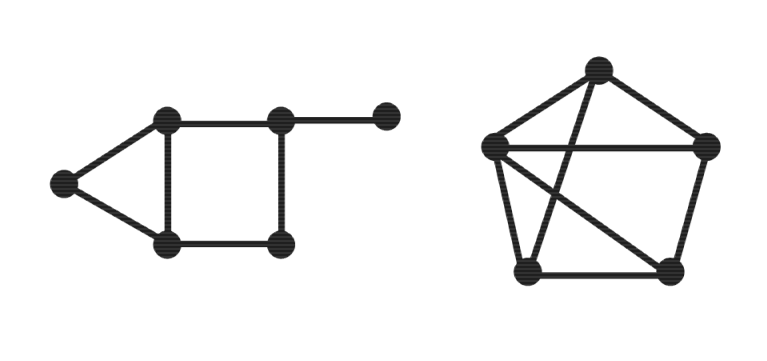
Before discussing the maxcut problem, it is necessary to provide some background information regarding relevant concepts in graph theory, the most fundamental of which is the graph itself. A graph is an ordered pair comprised of a set of vertices V and a set of edges E that connect pairs of distinct vertices in V . Two examples are shown in [link] . Graphs may be either weighted, in which a real value is assigned to each edge, or unweighted, in which all edges have equal value. Although the former is more broadly applicable, further discussion will focus almost exclusively on the latter.
Unsurprisingly, a subgraph of graph is a graph with vertex set and edge set . Of particular usefulness will be the subgraph of induced by a given set of edges , known as edge induced subgraph, which consists of that given set of edges E 1 along with all vertices that occur as an endpoint of at least one edge in E 1 . An example of an edge induced subgraph is shown in [link] .

One class of graphs that will be especially important to discussion of the maxcut problem is bipartite graphs. A graph is bipartite, like the example in [link] , if there are sets such that , , and only if or . Additionally, a graph is bipartite if and only if it has no subgraph that is a cycle of odd length.

A cut of a graph can be informally understood and visualized as a closed curve crossing some realization of the graph where each edge can be crossed at most once, as seen in [link] . Notice that the curve partitions the graph vertices into two disjoint subsets located to each side of the curve.

Notification Switch
Would you like to follow the 'The art of the pfug' conversation and receive update notifications?