| << Chapter < Page | Chapter >> Page > |
Triple integrals can often be more readily evaluated by using cylindrical coordinates instead of rectangular coordinates. Some common equations of surfaces in rectangular coordinates along with corresponding equations in cylindrical coordinates are listed in [link] . These equations will become handy as we proceed with solving problems using triple integrals.
| Circular cylinder | Circular cone | Sphere | Paraboloid | |
|---|---|---|---|---|
| Rectangular | ||||
| Cylindrical |
As before, we start with the simplest bounded region in to describe in cylindrical coordinates, in the form of a cylindrical box, ( [link] ). Suppose we divide each interval into subdivisions such that and Then we can state the following definition for a triple integral in cylindrical coordinates.
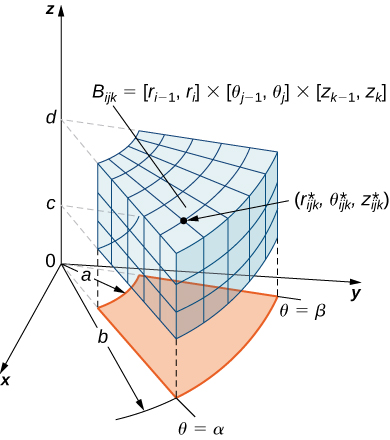
Consider the cylindrical box (expressed in cylindrical coordinates)
If the function is continuous on and if is any sample point in the cylindrical subbox ( [link] ), then we can define the triple integral in cylindrical coordinates as the limit of a triple Riemann sum, provided the following limit exists:
Note that if is the function in rectangular coordinates and the box is expressed in rectangular coordinates, then the triple integral is equal to the triple integral and we have
As mentioned in the preceding section, all the properties of a double integral work well in triple integrals, whether in rectangular coordinates or cylindrical coordinates. They also hold for iterated integrals. To reiterate, in cylindrical coordinates, Fubini’s theorem takes the following form:
Suppose that is continuous on a rectangular box which when described in cylindrical coordinates looks like
Then and
The iterated integral may be replaced equivalently by any one of the other five iterated integrals obtained by integrating with respect to the three variables in other orders.
Cylindrical coordinate systems work well for solids that are symmetric around an axis, such as cylinders and cones. Let us look at some examples before we define the triple integral in cylindrical coordinates on general cylindrical regions.
Evaluate the triple integral where the cylindrical box is
As stated in Fubini’s theorem, we can write the triple integral as the iterated integral
The evaluation of the iterated integral is straightforward. Each variable in the integral is independent of the others, so we can integrate each variable separately and multiply the results together. This makes the computation much easier:

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?