Wiskunde
Gewone breuke
Opvoeders afdeling
Memorandum
10
10
1
10
size 12{ { { size 8{1} } over { size 8{"10"} } } } {}
1
10
size 12{ { { size 8{1} } over { size 8{"10"} } } } {}
Answers is the same
(i) =
3
4
size 12{ { { size 8{3} } over { size 8{4} } } } {} x
1
2
size 12{ { { size 8{1} } over { size 8{2} } } } {}
x =
3
8
size 12{ { { size 8{3} } over { size 8{8} } } } {}
y = 18
2
3
size 12{ { { size 8{2} } over { size 8{3} } } } {}
(ii) = 7 x
8
3
size 12{ { { size 8{8} } over { size 8{3} } } } {}
=
56
3
size 12{ { { size 8{"56"} } over { size 8{3} } } } {}
=
6
1
size 12{ { { size 8{6} } over { size 8{1} } } } {} x
5
4
size 12{ { { size 8{5} } over { size 8{4} } } } {}
=
30
4
size 12{ { { size 8{"30"} } over { size 8{4} } } } {}
m = 7
1
2
size 12{ { { size 8{1} } over { size 8{2} } } } {}
(iv) =
2
7
size 12{ { { size 8{2} } over { size 8{7} } } } {} x
1
9
size 12{ { { size 8{1} } over { size 8{9} } } } {}
n =
2
63
size 12{ { { size 8{2} } over { size 8{"63"} } } } {}
(i)
x =
3
8
size 12{ { { size 8{3} } over { size 8{8} } } } {}
9
24
size 12{ { { size 8{9} } over { size 8{"24"} } } } {}
=
3
8
size 12{ { { size 8{3} } over { size 8{8} } } } {} x
24
9
size 12{ { { size 8{"24"} } over { size 8{9} } } } {}
x = 1
(ii)
k =
15
18
size 12{ { { size 8{"15"} } over { size 8{"18"} } } } {}
45
6
size 12{ { { size 8{"45"} } over { size 8{6} } } } {}
=
15
18
size 12{ { { size 8{"15"} } over { size 8{"18"} } } } {} x
6
45
size 12{ { { size 8{6} } over { size 8{"45"} } } } {}
k =
1
9
size 12{ { { size 8{1} } over { size 8{9} } } } {}
(iii)
c =
7
9
size 12{ { { size 8{7} } over { size 8{9} } } } {}
5
6
size 12{ { { size 8{5} } over { size 8{6} } } } {}
=
7
9
size 12{ { { size 8{7} } over { size 8{9} } } } {} x
6
5
size 12{ { { size 8{6} } over { size 8{5} } } } {}
c =
14
15
size 12{ { { size 8{"14"} } over { size 8{"15"} } } } {}
(iv)
f =
11
12
size 12{ { { size 8{"11"} } over { size 8{"12"} } } } {}
6
5
size 12{ { { size 8{6} } over { size 8{5} } } } {}
=
11
12
size 12{ { { size 8{"11"} } over { size 8{"12"} } } } {} x
5
6
size 12{ { { size 8{5} } over { size 8{6} } } } {}
55
72
size 12{ { { size 8{"55"} } over { size 8{"72"} } } } {}
23.3 c)
(i)
b =
2
1
4
size 12{2 { { size 8{1} } over { size 8{4} } } } {}
3
2
size 12{ { { size 8{3} } over { size 8{2} } } } {}
=
9
4
size 12{ { { size 8{9} } over { size 8{4} } } } {} x
2
3
size 12{ { { size 8{2} } over { size 8{3} } } } {}
b = 1
1
2
size 12{ { { size 8{1} } over { size 8{2} } } } {}
(ii)
e = 3
4
5
size 12{ { { size 8{4} } over { size 8{5} } } } {} 2
1
2
size 12{ { { size 8{1} } over { size 8{2} } } } {}
=
19
5
size 12{ { { size 8{"19"} } over { size 8{5} } } } {} x
2
5
size 12{ { { size 8{2} } over { size 8{5} } } } {}
e =
38
25
size 12{ { { size 8{"38"} } over { size 8{"25"} } } } {}
e = 1
13
25
size 12{ { { size 8{"13"} } over { size 8{"25"} } } } {}
g = 3
4
7
size 12{ { { size 8{4} } over { size 8{7} } } } {} 1
2
7
size 12{ { { size 8{2} } over { size 8{7} } } } {}
=
25
7
size 12{ { { size 8{"25"} } over { size 8{7} } } } {} x
7
9
size 12{ { { size 8{7} } over { size 8{9} } } } {}
=
25
9
size 12{ { { size 8{"25"} } over { size 8{9} } } } {}
g = 2
7
9
size 12{ { { size 8{7} } over { size 8{9} } } } {}
(iv)
r = 15
1
2
size 12{ { { size 8{1} } over { size 8{2} } } } {} 5
1
4
size 12{ { { size 8{1} } over { size 8{4} } } } {}
=
31
2
size 12{ { { size 8{"31"} } over { size 8{2} } } } {} x
4
21
size 12{ { { size 8{4} } over { size 8{"21"} } } } {}
=
62
21
size 12{ { { size 8{"62"} } over { size 8{"21"} } } } {}
r = 2
20
21
size 12{ { { size 8{"20"} } over { size 8{"21"} } } } {}
Leerders afdeling
Inhoud
Aktiwiteit: deling met breuke [lu 1.7.3, lu 2.1.5]
23. Kom ons kyk nou na DELING MET BREUKE!
23.1
Deling van heelgetalle deur breuke en andersom :
a) Werk saam met ’n maat en kyk goed na die volgende probleme.
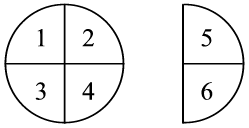
Ma bak vyf koeke en wil graag vir jou en jou maats elkeen ’n halwe (
1
2
size 12{ { { size 8{1} } over { size 8{2} } } } {} ) stuk gee. Hoeveel maats kan van die koek eet?
Op ’n getallelyn lyk dit so:
Dus: 5 ÷
1
2
size 12{ { { size 8{1} } over { size 8{2} } } } {} = 1010 kinders kan elkeen
1
2
size 12{ { { size 8{1} } over { size 8{2} } } } {} koek kry.
Ma bak weer, maar hierdie keer net een reghoekige koek. Sy besluit om die helfte daarvan tussen haar vyf kinders te verdeel. Watter breuk kry elkeen?
Kom ons maak ’n skets daarvan!
12345
Kan jy sien dat elke kind een tiende (
1
10
size 12{ { { size 8{1} } over { size 8{"10"} } } } {} ) van die koek sal kry?Dus:
1
2
size 12{ { { size 8{1} } over { size 8{2} } } } {} ÷ 5 =
1
10
size 12{ { { size 8{1} } over { size 8{"10"} } } } {}
b) Voltooi die tabel:
5 ÷
1
2
size 12{ { { size 8{1} } over { size 8{2} } } } {} = ............
5 ×
2
1
size 12{ { { size 8{2} } over { size 8{1} } } } {} = ............
1
2
size 12{ { { size 8{1} } over { size 8{2} } } } {} ÷
5
1
size 12{ { { size 8{5} } over { size 8{1} } } } {} = ............
1
2
size 12{ { { size 8{1} } over { size 8{2} } } } {} ×
1
5
size 12{ { { size 8{1} } over { size 8{5} } } } {} = ............
Wat merk jy op? ___________________________________________________
_____________________________________________________________________
c) Het jy geweet?
Enige deelsom met breuke kan in ’n vermenigvuldigingsom verander word! Ons doen dit deur die
deler in sy
resiprook te verander. Ons
“keer dus die deler om”!
Dus:
÷
1
2
size 12{ { { size 8{1} } over { size 8{2} } } } {} =
´
2
1
size 12{ { { size 8{2} } over { size 8{1} } } } {} = 10
d) Verbind kolom A met die korrekte antwoord in kolom B:
A
B
÷ deur 5
× met
4
3
size 12{ { { size 8{4} } over { size 8{3} } } } {}
÷ deur
3
4
size 12{ { { size 8{3} } over { size 8{4} } } } {}
× met 3
÷ deur
7
8
size 12{ { { size 8{7} } over { size 8{8} } } } {}
× met 5
÷ deur
1
3
size 12{ { { size 8{1} } over { size 8{3} } } } {}
× met
1
5
size 12{ { { size 8{1} } over { size 8{5} } } } {}
÷ deur
1
5
size 12{ { { size 8{1} } over { size 8{5} } } } {}
× met
8
7
size 12{ { { size 8{8} } over { size 8{7} } } } {}
e) Bereken die volgende:
i)
x
=
3
4
÷
2
size 12{x= { { size 8{3} } over { size 8{4} } } div 2} {}
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
ii)
y
=
7
÷
3
8
size 12{y=7 div { { size 8{3} } over { size 8{8} } } } {}
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
iii)
m
=
6
÷
4
5
size 12{m=6 div { { size 8{4} } over { size 8{5} } } } {}
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
iv)
n
=
2
7
÷
9
size 12{n= { { size 8{2} } over { size 8{7} } } div 9} {}
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
23.2
Deling van breuke deur breuke:
a) Werk weer saam met ’n maat en bestudeer die volgende:
x
=
6
25
÷
3
5
size 12{x= { { size 8{6} } over { size 8{"25"} } } div { { size 8{3} } over { size 8{5} } } } {}
Ek weet ek moet die volgende stappe volg:
1. Verander die ÷ in
×
2. Draai die breuk na die ÷ (deler) om – kry dus resiprook
3. Vermenigvuldig soos gewoonlik:
teller
×
teller
noemer
×
noemer
size 12{ { { ital "teller" times ital "teller"} over { ital "noemer" times ital "noemer"} } } {}
Dus:
6
25
÷
3
5
=
6
25
×
5
3
size 12{ { { size 8{6} } over { size 8{"25"} } } div { { size 8{3} } over { size 8{5} } } = { { size 8{6} } over { size 8{"25"} } } times { { size 8{5} } over { size 8{3} } } } {}
Ek kanselleer waar ek kan:
2
6
5
25
×
5
1
3
1
Die antwoord is dus
2
×
1
5
×
1
=
2
5
size 12{ { { size 8{2 times 1} } over { size 8{5 times 1} } } = { { size 8{2} } over { size 8{5} } } } {}
b) Probeer die volgende op jou eie:
i)
x
=
3
8
÷
9
24
size 12{x= { { size 8{3} } over { size 8{8} } } div { { size 8{9} } over { size 8{"24"} } } } {}
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
ii)
k
=
15
18
÷
45
6
size 12{k= { { size 8{"15"} } over { size 8{"18"} } } div { { size 8{"45"} } over { size 8{6} } } } {}
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
iii)
c
=
7
9
÷
5
6
size 12{c= { { size 8{7} } over { size 8{9} } } div { { size 8{5} } over { size 8{6} } } } {}
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
iv)
f
=
11
12
÷
6
5
size 12{f= { { size 8{"11"} } over { size 8{"12"} } } div { { size 8{6} } over { size 8{5} } } } {}
___________________________________________________
___________________________________________________
___________________________________________________
___________________________________________________
23.3
Deling met gemengde getalle:
a) Kan jy die volgende probleem vir ’n maat verduidelik?
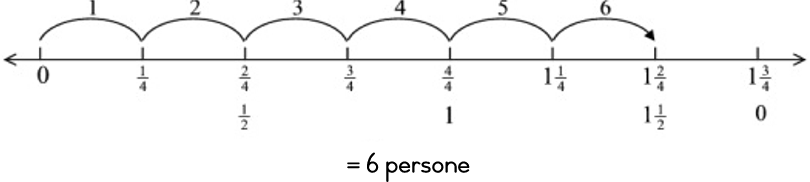
’n Gesin eet 1 en ’n halwe (
1
1
2
size 12{1 { { size 8{1} } over { size 8{2} } } } {} ) pizza. As elkeen net een kwart (
1
4
size 12{ { { size 8{1} } over { size 8{4} } } } {} ) van die pizza eet, uit hoeveel lede bestaan die gesin?
Ek moet 1
1
2
size 12{ { { size 8{1} } over { size 8{2} } } } {} ÷
1
4
size 12{ { { size 8{1} } over { size 8{4} } } } {} bereken.
Dis makliker as ek dit teken:
It’s easier if I draw it:
Die antwoord is dus 6.
Wiskundig skryf ek dit so:
y
=
1
1
2
÷
1
4
3
2
÷
1
4
3
2
×
4
1
12
2
6
alignl { stack {
size 12{y=1 { { size 8{1} } over { size 8{2} } } div { { size 8{1} } over { size 8{4} } } } {} #= { { size 8{3} } over { size 8{2} } } div { { size 8{1} } over { size 8{4} } } {} #
= { { size 8{3} } over { size 8{2} } } times { { size 8{4} } over { size 8{1} } } {} #= { { size 8{"12"} } over { size 8{2} } } {} #
=6 {}} } {}
Ek verkies om ’n getallelyn te gebruik:
b)
Het jy geweet?
Ons verander
gemengde getalle eers in
onegte breuke voordat ons die antwoord bereken.
c) Probeer op jou eie:
i)
b
=
2
1
4
÷
3
2
size 12{b=2 { { size 8{1} } over { size 8{4} } } div { { size 8{3} } over { size 8{2} } } } {}
___________________________________________________
___________________________________________________
___________________________________________________
ii)
e
=
3
4
5
÷
2
1
2
size 12{e=3 { { size 8{4} } over { size 8{5} } } div 2 { { size 8{1} } over { size 8{2} } } } {}
___________________________________________________
___________________________________________________
___________________________________________________
iii)
g
=
3
4
7
÷
1
2
7
size 12{g=3 { { size 8{4} } over { size 8{7} } } div 1 { { size 8{2} } over { size 8{7} } } } {}
___________________________________________________
___________________________________________________
___________________________________________________
iv)
r
=
15
1
2
÷
5
1
4
size 12{r="15" { { size 8{1} } over { size 8{2} } } div 5 { { size 8{1} } over { size 8{4} } } } {}
___________________________________________________
___________________________________________________
___________________________________________________
Assessering
Leeruitkomste 1: Die leerder is in staat om getalle en die verwantskappe daarvan te herken, te beskryf en voor te stel, en om tydens probleemoplossing bevoeg en met selfvertroue te tel, te skat, te bereken en te kontroleer.
Assesseringstandaard 1.7: Dit is duidelik wanneer die leerder skat en bereken deur geskikte bewerkings vir probleme wat die volgende behels, kies en gebruik:
1.7.3: optelling, aftrekking en vermenigvuldiging van gewone breuke.
Leeruitkomste 2: Die leerder is in staat om patrone en verwantskappe te herken, te beskryf en voor te stel en probleme op te los deur algebraïese taal en vaardighede te gebruik.
Assesseringstandaard 2.1: Dit is duidelik wanneer die leerder numeriese en meetkundige patrone ondersoek en uitbrei op soek na ‘n verwantskap of reëls, insluitend patrone;
2.1.5: voorgestel in tabelle.