| << Chapter < Page | Chapter >> Page > |
Recognizing that the occurs when is zero and that the occurs when is zero gives us a method to find the intercepts of a line from its equation. To find the let and solve for To find the let and solve for
Use the equation to find:
| x | y |
|---|---|
| 0 | |
| 0 |
Find the intercepts of
We'll fill in [link] .

To find the x- intercept, let :
|
| |
| Substitute 0 for y . |
|
| Add. |
|
| Divide by 2. |
|
| The x -intercept is (3, 0). |
To find the y- intercept, let :
|
| |
| Substitute 0 for x . |
|
| Multiply. |
|
| Add. |
|
| The y -intercept is (0, 6). |
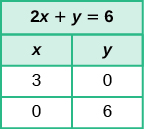
The intercepts are the points and as shown in the chart.
Find the intercepts of
To find the let
| Distribute 0 for | |
| Multiply. | |
| Subtract. | |
| Divide by 4. |
The is
To find the let
| Substitute 0 for | |
| Multiply. | |
| Simplify. | |
| Divide by −3. |
The is
The intercepts are the points and
| x | y |
Find the intercepts of the line:
x -intercept (4,0); y -intercept: (0,−3)
Find the intercepts of the line:
x -intercept (4,0); y -intercept: (0,−2)
To graph a linear equation by plotting points, you can use the intercepts as two of your three points. Find the two intercepts, and then a third point to ensure accuracy, and draw the line. This method is often the quickest way to graph a line.
Graph using intercepts.
First, find the Let
The is
Now find the Let
The is
Find a third point. We’ll use
A third solution to the equation is
Summarize the three points in a table and then plot them on a graph.
| x | y | (x,y) |
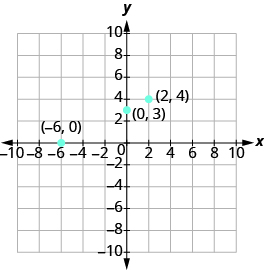
Do the points line up? Yes, so draw line through the points.
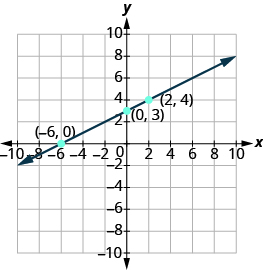
Graph using intercepts.
Find the intercepts and a third point.

We list the points and show the graph.
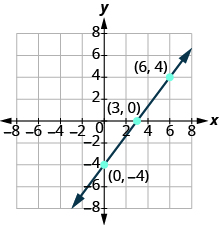
Graph using the intercepts.

This line has only one intercept! It is the point
To ensure accuracy, we need to plot three points. Since the intercepts are the same point, we need two more points to graph the line. As always, we can choose any values for
so we’ll let
be
and
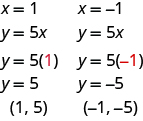
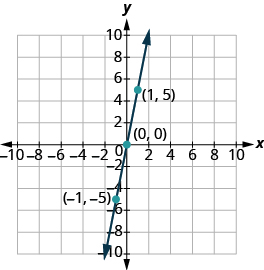
Organize the points in a table.
Plot the three points, check that they line up, and draw the line.

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?