| << Chapter < Page | Chapter >> Page > |
Vir funksie van die vorm , word die metode om die afsnitte met die as te bereken gegee.
Die -afsnit word bereken as volg: stel
In die vergelyking , is 'n konstante en het verskillende effekte op die grafiek van die funksie. Die algemene vorm van die grafiek van hierdie soort funksies word gegee in [link] for the function .
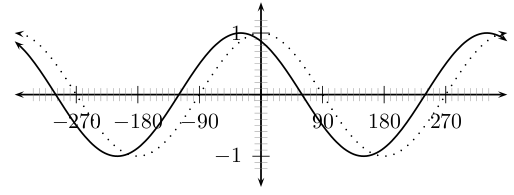
Op dieselfde assestelsel, plot die volgende grafieke:
Gebruik jou resultate om die effek van af te lei.
Jy sal vind dat die waarde van affekteer die -afsnit en die fase skuif van die grafiek. Soos in die geval van die sinus grafiek, positiewe waardes van skuif die cosinus grafiek links, terwyl negatiewe waardes skuif die grafiek regs.
Die verskillende eienskappe word opgesom in [link] .
|
|
|
Vir is die definisie versameling , omdat daar geen waarde is van waarvoor ongedefinieerd is nie.
Die waarde versameling van is .
Vir funksies van die vorm , word die metode om die afsnit met die as te kry gegee.
Die -afsnite word bereken as volg: stel
In die vergelyking , is 'n konstante en het verskeie effekte op die grafiek van die funksie. Die algemene vorm van grafieke van funksies in die vorm word gegee in [link] for the function .
Op dieselfde assestelsel, plot die volgende grafieke:
Gebruik jou resultate om die effek van af te lei.
Jy behoort te vind dat die waarde van affekteer weereens die -afsnit en die fase skuif van die grafiek. Daar is 'n horisontale skuif na links indien positief is en na regs indien negatief is.
Die verskillende eienskappe word opgesom in [link] .
|
|
|
Vir is die definisie versameling van een tak , omdat die funksie ongedefinieerd is vir en .
Die waarde versameling van is .
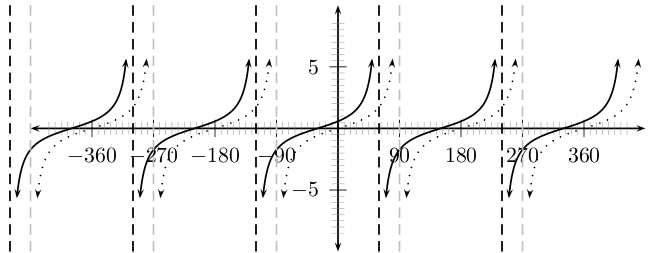
Vir funksies van die vorm word die metode om die afsnitte met die as te bereken gegee.
Die -afsnit word as volg bereken: stel
Die grafiek van het asimtote, omdat soos benader, benader oneindig. Daar is dus geen gedefinieerde waarde vir die funksie by die asimtoot waardes nie.
Gebruik jou kennis van die effekte van en teken 'n rowwe skets van die volgende funksies, sonder om 'n tabel van waardes te gebruik.

Notification Switch
Would you like to follow the 'Siyavula textbooks: wiskunde (graad 11)' conversation and receive update notifications?