1. Home
  2. Software receiver design
  3. Software receiver design
  4. Carrier recovery

0.9 Carrier recovery  (Page 19/19)

<< Chapter < Page
  Software receiver design     Page 19 / 19
Chapter >> Page >
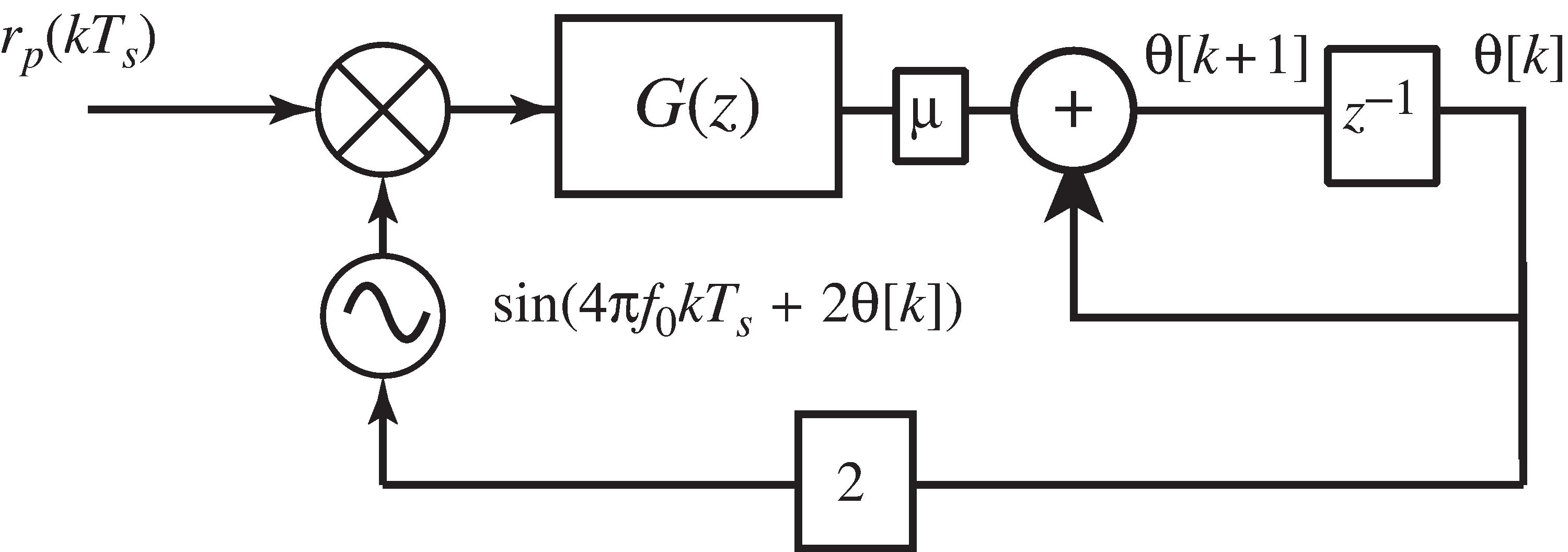
The general PLL can track both phase and frequency offsets using an IIR LPFG(z). This figure is identical to Figure 10-7, except that the FIR lowpass filter is replaced by a suitable IIR lowpass filter. Linearizing this structure gives Figure 10-23. Appendix F presents conditions on G(z) under which the tracking occurs.
The general PLL can track both phase and frequency offsets using an IIR LPF G ( z ) . This figure is identical to [link] , except that the FIR lowpass filter is replaced by a suitable IIRlowpass filter. Linearizing this structure gives [link] .

To see the operation of the generalized PLL concretely, pllgeneral.m implements the system of [link] with G N ( z ) = 2 - μ - 2 z and G D ( z ) = z - 1 . The implementation of the IIR filter follows the time domainmethod in waystofiltIIR.m . When the frequency offset is zero (when f0=fc ), theta converges to phoff . When there is a frequency offset (as in the default values with f0=fc+0.1 ), theta converges to a line. 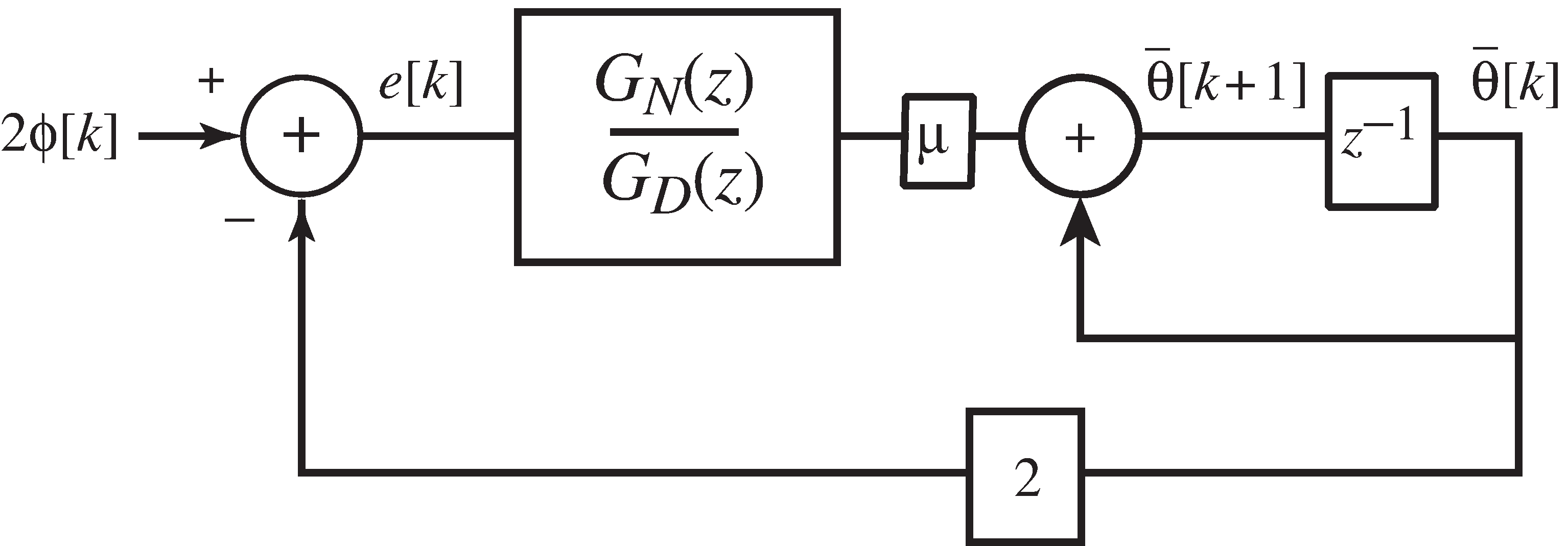Essentially, this θ value converges to θ 1 + θ 2 in the dual loop structure of [link] .

Ts=1/10000; time=1; t=Ts:Ts:time;       % time vector fc=1000; phoff=-0.8;                    % carrier freq. and phaserp=cos(4*pi*fc*t+2*phoff);              % simplified received signal mu=.003;                                % algorithm stepsizea=[1 -1]; lena=length(a)-1;             % autoregressive coefficientsb=[-2 2-mu]; lenb=length(b);            % moving average coefficientsxvec=zeros(lena,1); evec=zeros(lenb,1);  % initial states in filter f0=1000.1;                              % assumed freq. at receivertheta=zeros(1,length(t)); theta(1)=0;   % initialize vector for estimates for k=1:length(t)-1                     % z contains past fl+1 inputs    e=rp(k)*sin(4*pi*f0*t(k)+2*theta(k));     evec=[e;evec(1:end-1)];             % past values of inputs     x=-a(2:end)*xvec+b*evec;            % output of filter    xvec=[x;xvec(1:end-1)];             % past values of outputs    theta(k+1)=theta(k)+mu*x;           % algorithm update end
pllgeneral.m the PLL with an IIR LPF (download file)

All of the PLL structures are nonlinear, which makes them hard to analyze exactly.One way to study the behavior of a nonlinear system is to replace nonlinear components with nearby linear elements.A linearization is only valid for a small range of values. For example, the nonlinear function sin ( x ) is approximately x for small values. This can be seen by looking at sin ( x ) near the origin: it is approximately a line with slope one. As x increases or decreases away from the origin, the approximation worsens.

The nonlinear components in a loop structure such as [link] are the oscillators and the mixers.Consider a non-ideal lowpass filter F ( z ) with impulse response f [ k ] that has a cutoff frequency below 2 f 0 . The output of the LPF is e [ k ] = f [ k ] * sin ( 2 θ [ k ] - 2 Φ [ k ] ) where * represents convolution. With Φ ˜ ≡ θ - Φ and Φ ≈ θ , sin ( 2 Φ ˜ [ k ] ) ≈ 2 Φ ˜ [ k ] . Thus the linearization is

f [ k ] * sin ( 2 Φ ˜ [ k ] ) ≈ f [ k ] * 2 Φ ˜ [ k ] .

In words, applying a LPF to sin ( x ) is approximately the same as applying the LPF to x , at least for sufficiently small x .

There are two ways to understand why the general PLL structure in [link] works, both of which involve linearization arguments.The first method linearizes [link] and applies the final value theorem for Z -transforms. The second method is toshow that a linearization of the generalized single-loop structure of [link] is the same as a linearization of the dual-loop method of [link] , at least for certain values of the parameters. [link] shows that for certain special cases, the two strategies (the dual-loop and the generalized single-loop)behave similarly in the sense that both have the same linearization.

What is the largest frequency offset that pllgeneral.m can track? How does theta behave when the tracking fails?

Examine the effect of different filters in pllgeneral.m .

  1. Show that the filter used in pllgeneral.m has a lowpass character.
  2. Let a=[1 0] . What kind of IIR filter does this represent? How does the loop behave for a frequency offset?
  3. Can you choose b so that the loop fails?
  4. Design an IIR a and b pair using cheby1 or cheby2 . Test whether the loop functions to track small frequency offsets.

Design the equivalent squared difference loop, combining the IIR structure of pllgeneral.m with the squared difference objective function as in pllsd.m .

Design the equivalent general Costas loop structure. Hint: replace the FIR LPFs in [link] with suitable IIR filters. Create a simulation to verify the operation of the method.

The code in pllgeneral.m is simplified in the sense that the received signal rp contains just the unmodulated carrier. Implement a more realistic scenario by combining pulrecsig.m to include a binary message sequence, pllpreprocess.m to create rp , and pllgeneral.m to recover the unknown phase offset of the carrier. Demonstrate that the same systemcan track a frequency offset.

Investigate how the method performs when the received signal contains pulse shaped 4-PAM data.Verify that it can track both phase and frequency offsets.

This exercise outlines the steps needed to show the conditions under which the general PLL of [link] and the dual loop structure of [link] are the same (in the sense of having the same linearization).

  1. Show that [link] is the linearization of [link] .
    A linearization of the dual-loop frequency tracker of Figure 10-19. For small offsets, this linear structure closely represents the behavior of the system.
    A linearization of the dual-loop frequency tracker of [link] . For small offsets, this linear structure closely represents the behavior of the system.
  2. Show that [link] is the linearization of the general PLL of [link] .
    This is the linearization of Figure 10-21.
    This is the linearization of [link] .
  3. Show that the two block diagrams in [link] are the same.
    The top block diagram with overlapping loops can be redrawn as the bottom split diagram.
    The top block diagram with overlapping loops can be redrawn as the bottom split diagram.
  4. Suppose that the lowpass filters are ideal: F 1 ( z ) = F 2 ( z ) = 1 for all frequencies below the cutoff and F 1 ( z ) = F 2 ( z ) = 0 at all frequencies above. Make the following assignments:
    A = μ z - 1 + 2 μ B = μ z - 1 C = 2
    Using the block diagram manipulation of part (c), show that [link] and [link] are the same when
    G N ( z ) = μ ( 2 z - 2 + 2 μ ) G N ( z ) = z - 1 .

For further reading

  • J.P. Costas, “Synchronous Communications," Proceedings of the IRE , pp. 1713–1718, Dec. 1956.
  • L. E. Franks, “Carrier and Bit Synchronization in Data Communication—A Tutorial Review,” IEEE Transactions on Communications , vol. COM-28, no. 8, pp. 1107–1120, August 1980.
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Software receiver design. OpenStax CNX. Aug 13, 2013 Download for free at http://cnx.org/content/col11510/1.3
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Software receiver design' conversation and receive update notifications?

Ask