Home
Econometrics for honors students Background issues in statistics Statistical terminology
Log normal distribution. The continuous random variable
x has log normal distribution if
y has a normal distribution and
x
=
e
y
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIhacqGH9aqpcaWGLbWaaWbaaSqabeaacaWG5baaaOGaaiOlaaaa@3ABD@ Thus, if
y
∼
N
(
μ
,
σ
2
)
,
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMhacqWI8iIocaWGobWaaeWaaeaacqaH8oqBcaGGSaGaeq4Wdm3aaWbaaSqabeaacaaIYaaaaaGccaGLOaGaayzkaaGaaiilaaaa@4038@ then the pdf of a log normal distribution is
f
(
x
)
=
{
1
x
σ
2
π
e
−
(
ln
(
x
)
−
μ
)
2
2
σ
2
, for
x
>
0
0
otherwise
}
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAgadaqadaqaaiaadIhaaiaawIcacaGLPaaacqGH9aqpdaGadaabaeqabaWaaSaaaeaacaaIXaaabaGaamiEaiabeo8aZnaakaaabaGaaGOmaiabec8aWbWcbeaaaaGccaWGLbWaaWbaaSqabeaacqGHsisldaWcaaqaamaabmaabaGaciiBaiaac6gadaqadaqaaiaadIhaaiaawIcacaGLPaaacqGHsislcqaH8oqBaiaawIcacaGLPaaadaahaaadbeqaaiaaikdaaaaaleaacaaIYaGaeq4Wdm3aaWbaaWqabeaacaaIYaaaaaaaaaGccaqGSaGaaeiiaiaabccacaqGMbGaae4BaiaabkhacaqGGaGaamiEaiabg6da+iaaicdaaeaacaaIWaGaaeiiaiaabccacaqGGaGaaeiiaiaab+gacaqG0bGaaeiAaiaabwgacaqGYbGaae4DaiaabMgacaqGZbGaaeyzaaaacaGL7bGaayzFaaGaaiOlaaaa@6667@ The mean and variance of
x are
μ
x
=
e
μ
+
σ
2
2
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabeY7aTnaaBaaaleaacaWG4baabeaakiabg2da9iaadwgadaahaaWcbeqaaiabeY7aTjabgUcaRmaaleaameaacqaHdpWCdaahaaqabeaacaaIYaaaaaqaaiaaikdaaaaaaaaa@4101@ and
σ
x
2
=
(
e
σ
2
−
1
)
e
2
μ
+
σ
2
.
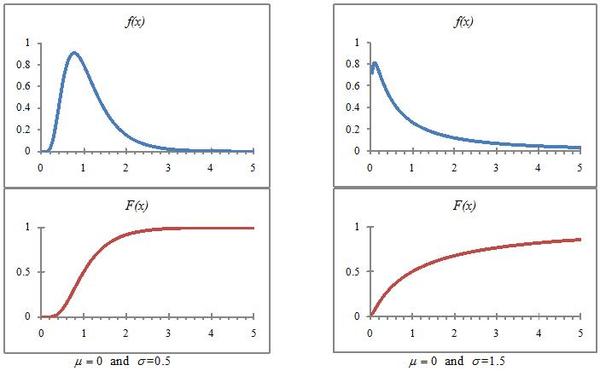
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabeo8aZnaaDaaaleaacaWG4baabaGaaGOmaaaakiabg2da9maabmaabaGaamyzamaaCaaaleqabaGaeq4Wdm3aaWbaaWqabeaacaaIYaaaaaaakiabgkHiTiaaigdaaiaawIcacaGLPaaacaWGLbWaaWbaaSqabeaacaaIYaGaeqiVd0Maey4kaSIaeq4Wdm3aaWbaaWqabeaacaaIYaaaaaaakiaac6caaaa@4975@ Because the distribution is skewed downward for variances over 1, the log normal distribution is sometimes used to describe income distributions (where there are relatively few very wealthy people and incomes generally are positive. Figure 4 shows the graphs of the pdf and cumulative functions for the log normal distributions for two values of
σ .
The log-normal distribution.
The two panels illustrate the log-normal distribution for two values of
σ ..
Gamma distribution. A positive random variable
x has a gamma distribution if its pdf is
f
(
x
)
=
1
Γ
(
α
)
β
α
x
α
−
1
e
−
x
β
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAgadaqadaqaaiaadIhaaiaawIcacaGLPaaacqGH9aqpdaWcaaqaaiaaigdaaeaacqqHtoWrdaqadaqaaiabeg7aHbGaayjkaiaawMcaaiabek7aInaaCaaaleqabaGaeqySdegaaaaakiaadIhadaahaaWcbeqaaiabeg7aHjabgkHiTiaaigdaaaGccaWGLbWaaWbaaSqabeaacqGHsisldaWcbaadbaGaamiEaaqaaiabek7aIbaaaaaaaa@4C6C@ for
x
>
0
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIhacqGH+aGpcaaIWaaaaa@38A8@ and 0 elsewhere.
Γ
(
α
)
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabfo5ahnaabmaabaGaeqySdegacaGLOaGaayzkaaaaaa@3A79@ is known as the gamma function and is defined to be
Γ
(
α
)
=
∫
0
∞
y
α
−
1
e
−
y
d
y
=
(
α
−
1
)
!
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabfo5ahnaabmaabaGaeqySdegacaGLOaGaayzkaaGaeyypa0Zaa8qmaeaacaWG5bWaaWbaaSqabeaacqaHXoqycqGHsislcaaIXaaaaOGaamyzamaaCaaaleqabaGaeyOeI0IaamyEaaaakiaadsgacaWG5baaleaacaaIWaaabaGaeyOhIukaniabgUIiYdGccqGH9aqpdaqadaqaaiabeg7aHjabgkHiTiaaigdaaiaawIcacaGLPaaacaGGHaGaaiOlaaaa@5079@ The gamma function is often used to model waiting times like waiting for death. Its mean and variance are given by
μ
=
α
β
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabeY7aTjabg2da9iabeg7aHjabek7aIbaa@3BE5@ and
σ
2
=
α
β
2
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabeo8aZnaaCaaaleqabaGaaGOmaaaakiabg2da9iabeg7aHjabek7aInaaCaaaleqabaGaaGOmaaaakiaac6caaaa@3E8A@
Chi-square distribution. A chi-square distribution (
χ
2
(
k
)
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabeE8aJnaaCaaaleqabaGaaGOmaaaakmaabmaabaGaam4AaaGaayjkaiaawMcaaiaac6caaaa@3BBE@ ) is the sum of
k independent standard normal random variables and is a special case of the gamma distribution (with
α
=
k
2
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabeg7aHjabg2da9maalaaabaGaam4Aaaqaaiaaikdaaaaaaa@3A4A@ and
β
=
2
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabek7aIjabg2da9iaaikdaaaa@394C@ ). The pdf of a chi-square distribution with
k degrees of freedom is
f
(
x
)
=
1
2
k
2
Γ
(
k
2
)
x
k
2
−
1
e
−
x
2
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAgadaqadaqaaiaadIhaaiaawIcacaGLPaaacqGH9aqpdaWcaaqaaiaaigdaaeaacaaIYaWaaWbaaSqabeaadaWcdaadbaGaam4AaaqaaiaaikdaaaaaaOGaeu4KdC0aaeWaaeaadaWcbaWcbaGaam4AaaqaaiaaikdaaaaakiaawIcacaGLPaaaaaGaamiEamaaCaaaleqabaWaaSqaaWqaaiaadUgaaeaacaaIYaaaaSGaeyOeI0IaaGymaaaakiaadwgadaahaaWcbeqaaiabgkHiTmaaleaameaacaWG4baabaGaaGOmaaaaaaaaaa@4B36@ where
x >0. Its mean and variance are
μ
=
k
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabeY7aTjabg2da9iaadUgaaaa@3995@ and
σ
2
=
2
k
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabeo8aZnaaCaaaleqabaGaaGOmaaaakiabg2da9iaaikdacaWGRbGaaiOlaaaa@3C03@ If
y
=
∑
i
=
1
k
x
i
2
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMhacqGH9aqpdaaeWbqaaiaadIhadaqhaaWcbaGaamyAaaqaaiaaikdaaaaabaGaamyAaiabg2da9iaaigdaaeaacaWGRbaaniabggHiLdaaaa@4097@ where the
x
i 's are independently drawn from the standard normal distribution (N(1, 0)), then
y
i
∼
χ
2
(
k
)
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadMhadaWgaaWcbaGaamyAaaqabaGccqWI8iIocqaHhpWydaahaaWcbeqaaiaaikdaaaGcdaqadaqaaiaadUgaaiaawIcacaGLPaaacaGGUaaaaa@3F09@
Student's t-distribution. Consider two random variables,
x and
v . Assume that
x
∼
N
(
0
,
1
)
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIhacqWI8iIocaWGobWaaeWaaeaacaaIWaGaaiilaiaaigdaaiaawIcacaGLPaaaaaa@3C90@ and
v
∼
χ
2
(
r
)
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAhacqWI8iIocqaHhpWydaahaaWcbeqaaiaaikdaaaGcdaqadaqaaiaadkhaaiaawIcacaGLPaaaaaa@3D37@ and are stochastically independent. Then the random variable
t
=
w
v
r
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadshacqGH9aqpdaWcaaqaaiaadEhaaeaadaGcaaqaamaalaaabaGaamODaaqaaiaadkhaaaaaleqaaaaaaaa@3B11@ has the t-distribution with
r
degrees of freedom . The pdf and cumulative function of
t are
f
(
t
)
=
Γ
(
r
+
1
2
)
r
π
Γ
(
r
2
)
(
1
+
t
2
r
)
−
(
r
+
1
2
)
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAgadaqadaqaaiaadshaaiaawIcacaGLPaaacqGH9aqpdaWcaaqaaiabfo5ahnaabmaabaWaaSaaaeaacaWGYbGaey4kaSIaaGymaaqaaiaaikdaaaaacaGLOaGaayzkaaaabaWaaOaaaeaacaWGYbGaeqiWdahaleqaaOGaeu4KdC0aaeWaaeaadaWcaaqaaiaadkhaaeaacaaIYaaaaaGaayjkaiaawMcaaaaadaqadaqaaiaaigdacqGHRaWkdaWcaaqaaiaadshadaahaaWcbeqaaiaaikdaaaaakeaacaWGYbaaaaGaayjkaiaawMcaamaaCaaaleqabaGaeyOeI0YaaeWaaeaadaWcaaqaaiaadkhacqGHRaWkcaaIXaaabaGaaGOmaaaaaiaawIcacaGLPaaaaaaaaa@5466@ and
F
(
t
)
=
1
2
+
t
Γ
(
t
2
)
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAeadaqadaqaaiaadshaaiaawIcacaGLPaaacqGH9aqpdaWcaaqaaiaaigdaaeaacaaIYaaaaiabgUcaRiaadshacqqHtoWrdaqadaqaamaalaaabaGaamiDaaqaaiaaikdaaaaacaGLOaGaayzkaaGaaiOlaaaa@4306@ The mean and variance of the distribution are 0 for
r
>
1
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadkhacqGH+aGpcaaIXaaaaa@38A3@ and
r
r
−
2
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaalaaabaGaamOCaaqaaiaadkhacqGHsislcaaIYaaaaaaa@3990@ for
t
>
2
,
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadshacqGH+aGpcaaIYaGaaiilaaaa@3956@ respectively.
The t-distribution plays a prominent role in hypothesis testing that is well-known to all undergraduate economics majors.
F distribution. Consider two stochastically independent chi-square random variable such that
u
∼
χ
2
(
r
1
)
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadwhacqWI8iIocaqGhpWaaWbaaSqabeaacaaIYaaaaOWaaeWaaeaacaWGYbWaaSbaaSqaaiaaigdaaeqaaaGccaGLOaGaayzkaaaaaa@3DBD@ and
v
∼
χ
2
(
r
2
)
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAhacqWI8iIocaqGhpWaaWbaaSqabeaacaaIYaaaaOWaaeWaaeaacaWGYbWaaSbaaSqaaiaaikdaaeqaaaGccaGLOaGaayzkaaaaaa@3DBF@ and
u
,
v
>
0.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadwhacaGGSaGaamODaiabg6da+iaaicdacaGGUaaaaa@3B02@ The new random variable
f
=
u
r
1
v
r
2
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAgacqGH9aqpdaWcaaqaamaaliaabaGaamyDaaqaaiaadkhadaWgaaWcbaGaaGymaaqabaaaaaGcbaWaaSGaaeaacaWG2baabaGaamOCamaaBaaaleaacaaIYaaabeaaaaaaaaaa@3DCA@ has a F-distribution with
r
1
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadkhadaWgaaWcbaGaaGymaaqabaaaaa@37C7@ and
r
2
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadkhadaWgaaWcbaGaaGOmaaqabaaaaa@37C8@ degrees of freedom. The pdf for the F-distribution is
g
(
f
)
=
Γ
(
r
1
+
r
2
2
)
(
r
1
r
2
)
Γ
(
r
1
2
)
Γ
(
r
2
2
)
f
r
1
2
−
1
(
1
+
r
1
f
r
2
)
r
1
+
r
2
2
.
MathType@MTEF@5@5@+=feaagyart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadEgadaqadaqaaiaadAgaaiaawIcacaGLPaaacqGH9aqpdaWcaaqaaiabfo5ahnaabmaabaWaaSaaaeaacaWGYbWaaSbaaSqaaiaaigdaaeqaaOGaey4kaSIaamOCamaaBaaaleaacaaIYaaabeaaaOqaaiaaikdaaaaacaGLOaGaayzkaaWaaeWaaeaadaWcaaqaaiaadkhadaWgaaWcbaGaaGymaaqabaaakeaacaWGYbWaaSbaaSqaaiaaikdaaeqaaaaaaOGaayjkaiaawMcaaaqaaiabfo5ahnaabmaabaWaaSaaaeaacaWGYbWaaSbaaSqaaiaaigdaaeqaaaGcbaGaaGOmaaaaaiaawIcacaGLPaaacqqHtoWrdaqadaqaamaalaaabaGaamOCamaaBaaaleaacaaIYaaabeaaaOqaaiaaikdaaaaacaGLOaGaayzkaaaaamaalaaabaGaamOzamaaCaaaleqabaWaaSaaaeaacaWGYbWaaSbaaWqaaiaaigdaaeqaaaWcbaGaaGOmaaaacqGHsislcaaIXaaaaaGcbaWaaeWaaeaacaaIXaGaey4kaSYaaSaaaeaacaWGYbWaaSbaaSqaaiaaigdaaeqaaOGaamOzaaqaaiaadkhadaWgaaWcbaGaaGOmaaqabaaaaaGccaGLOaGaayzkaaWaaWbaaSqabeaadaWcaaqaaiaadkhadaWgaaadbaGaaGymaaqabaWccqGHRaWkcaWGYbWaaSbaaWqaaiaaikdaaeqaaaWcbaGaaGOmaaaaaaaaaOGaaiOlaaaa@6771@ The F-distribution is used in testing if population variances are equal and in performing likelihood ratio tests.
Multinomial distribution. Consider the
n random variables
x
1
,
x
2
,
⋯
,
x
n
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIhadaWgaaWcbaGaaGymaaqabaGccaGGSaGaamiEamaaBaaaleaacaaIYaaabeaakiaacYcacqWIVlctcaGGSaGaamiEamaaBaaaleaacaWGUbaabeaaaaa@3FE0@ where each variable has a normal distribution—that is,
x
i
∼
N
(
μ
i
,
σ
i
2
)
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIhadaWgaaWcbaGaamyAaaqabaGccqWI8iIocaWGobWaaeWaaeaacqaH8oqBdaWgaaWcbaGaamyAaaqabaGccaGGSaGaeq4Wdm3aa0baaSqaaiaadMgaaeaacaaIYaaaaaGccaGLOaGaayzkaaaaaa@42BD@ and the covariance between of the variables is
σ
i
j
=
E
[
(
x
i
−
μ
i
)
(
x
j
−
μ
j
.
)
]
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabeo8aZnaaBaaaleaacaWGPbGaamOAaaqabaGccqGH9aqpcaWGfbWaamWaaeaadaqadaqaaiaadIhadaWgaaWcbaGaamyAaaqabaGccqGHsislcqaH8oqBdaWgaaWcbaGaamyAaaqabaaakiaawIcacaGLPaaadaqadaqaaiaadIhadaWgaaWcbaGaamOAaaqabaGccqGHsislcqaH8oqBdaWgaaWcbaGaamOAaaqabaaakiaawIcacaGLPaaaaiaawUfacaGLDbaaaaa@4C65@ We can arrange the variances and covariances into a
n -by-
n matrix where
Σ
=
[
σ
1
2
σ
12
⋯
σ
1
n
σ
21
σ
2
2
⋯
σ
2
n
⋮
⋮
⋱
⋮
σ
n
1
σ
n
2
⋯
σ
n
2
]
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabfo6atjabg2da9maadmaabaqbaeqabqabaaaaaeaacqaHdpWCdaqhaaWcbaGaaGymaaqaaiaaikdaaaaakeaacqaHdpWCdaWgaaWcbaGaaGymaiaaikdaaeqaaaGcbaGaeS47IWeabaGaeq4Wdm3aaSbaaSqaaiaaigdacaWGUbaabeaaaOqaaiabeo8aZnaaBaaaleaacaaIYaGaaGymaaqabaaakeaacqaHdpWCdaqhaaWcbaGaaGOmaaqaaiaaikdaaaaakeaacqWIVlctaeaacqaHdpWCdaWgaaWcbaGaaGOmaiaad6gaaeqaaaGcbaGaeSO7I0eabaGaeSO7I0eabaGaeSy8I8eabaGaeSO7I0eabaGaeq4Wdm3aaSbaaSqaaiaad6gacaaIXaaabeaaaOqaaiabeo8aZnaaBaaaleaacaWGUbGaaGOmaaqabaaakeaacqWIVlctaeaacqaHdpWCdaqhaaWcbaGaamOBaaqaaiaaikdaaaaaaaGccaGLBbGaayzxaaaaaa@6816@ that is known as the variance-covariance matrix. Define the vector
(
x
−
μ
)
=
(
x
1
−
μ
1
⋮
x
n
−
μ
n
)
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaabmaabaGaaCiEaiabgkHiTiaahY7aaiaawIcacaGLPaaacqGH9aqpdaqadaqaauaabeqadeaaaeaacaWG4bWaaSbaaSqaaiaaigdaaeqaaOGaeyOeI0IaeqiVd02aaSbaaSqaaiaaigdaaeqaaaGcbaGaeSO7I0eabaGaamiEamaaBaaaleaacaWGUbaabeaakiabgkHiTiabeY7aTnaaBaaaleaacaWGUbaabeaaaaaakiaawIcacaGLPaaaaaa@4AA8@ and
(
x
−
μ
)
′
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaabmaabaGaaCiEaiabgkHiTiaahY7aaiaawIcacaGLPaaadaahaaWcbeqaaOGamai4gkdiIcaaaaa@3DC7@ as its transpose. Then,
(
x
−
μ
)
′
Σ
(
x
−
μ
)
=
∑
i
=
1
n
∑
j
=
1
n
(
x
i
−
μ
i
)
(
x
j
−
μ
j
)
σ
i
j
,
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaabmaabaGaaCiEaiabgkHiTiaahY7aaiaawIcacaGLPaaadaahaaWcbeqaaOGamai4gkdiIcaacaWHJoWaaeWaaeaacaWH4bGaeyOeI0IaaCiVdaGaayjkaiaawMcaaiabg2da9maaqahabaWaaabCaeaadaqadaqaaiaadIhadaWgaaWcbaGaamyAaaqabaGccqGHsislcqaH8oqBdaWgaaWcbaGaamyAaaqabaaakiaawIcacaGLPaaadaqadaqaaiaadIhadaWgaaWcbaGaamOAaaqabaGccqGHsislcqaH8oqBdaWgaaWcbaGaamOAaaqabaaakiaawIcacaGLPaaacqaHdpWCdaWgaaWcbaGaamyAaiaadQgaaeqaaaqaaiaadQgacqGH9aqpcaaIXaaabaGaamOBaaqdcqGHris5aaWcbaGaamyAaiabg2da9iaaigdaaeaacaWGUbaaniabggHiLdGccaGGSaaaaa@63E3@ where
σ
i
i
=
σ
i
2
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabeo8aZnaaBaaaleaacaWGPbGaamyAaaqabaGccqGH9aqpcqaHdpWCdaqhaaWcbaGaamyAaaqaaiaaikdaaaaaaa@3E5E@ If
|
Σ
|
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaaemaabaGaaC4OdaGaay5bSlaawIa7aaaa@3A3A@ is the determinant of the variance-covariance matrix, then the pdf for the joint distribution of these random variables is
f
(
x
1
,
x
2
,
…
,
x
n
)
=
1
(
2
π
)
n
/
2
|
Σ
|
1
2
e
−
1
2
(
x
−
μ
)
′
Σ
(
x
−
μ
)
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAgadaqadaqaaiaadIhadaWgaaWcbaGaaGymaaqabaGccaGGSaGaamiEamaaBaaaleaacaaIYaaabeaakiaacYcacqWIMaYscaGGSaGaamiEamaaBaaaleaacaWGUbaabeaaaOGaayjkaiaawMcaaiabg2da9maalaaabaGaaGymaaqaamaabmaabaGaaGOmaiabec8aWbGaayjkaiaawMcaamaaCaaaleqabaGaamOBaiaac+cacaaIYaaaaOWaaqWaaeaacaWHJoaacaGLhWUaayjcSdWaaWbaaSqabeaadaWccaqaaiaaigdaaeaacaaIYaaaaaaaaaGccaWGLbWaaWbaaSqabeaacqGHsisldaWcaaqaaiaaigdaaeaacaaIYaaaamaabmaabaGaaCiEaiabgkHiTiaahY7aaiaawIcacaGLPaaadaahaaadbeqaaSGamaiUgkdiIcaacaWHJoWaaeWaaeaacaWH4bGaeyOeI0IaaCiVdaGaayjkaiaawMcaaaaakiaac6caaaa@61FC@ If the random variables are stochastically independent the covariances are equal to 0 and the pdf becomes
f
(
x
1
,
x
2
,
…
,
x
n
)
=
1
(
2
π
)
n
/
2
(
∏
i
=
1
n
σ
1
2
)
1
2
e
−
1
2
∑
i
=
1
n
(
x
i
−
μ
i
)
2
σ
i
2
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAgadaqadaqaaiaadIhadaWgaaWcbaGaaGymaaqabaGccaGGSaGaamiEamaaBaaaleaacaaIYaaabeaakiaacYcacqWIMaYscaGGSaGaamiEamaaBaaaleaacaWGUbaabeaaaOGaayjkaiaawMcaaiabg2da9maalaaabaGaaGymaaqaamaabmaabaGaaGOmaiabec8aWbGaayjkaiaawMcaamaaCaaaleqabaGaamOBaiaac+cacaaIYaaaaOWaaeWaaeaadaqeWbqaaiabeo8aZnaaDaaaleaacaaIXaaabaGaaGOmaaaaaeaacaWGPbGaeyypa0JaaGymaaqaaiaad6gaa0Gaey4dIunaaOGaayjkaiaawMcaamaaCaaaleqabaWaaSGaaeaacaaIXaaabaGaaGOmaaaaaaaaaOGaamyzamaaCaaaleqabaGaeyOeI0YaaSaaaeaacaaIXaaabaGaaGOmaaaadaaeWbqaamaalaaabaWaaeWaaeaacaWG4bWaaSbaaWqaaiaadMgaaeqaaSGaeyOeI0IaeqiVd02aaSbaaWqaaiaadMgaaeqaaaWccaGLOaGaayzkaaWaaWbaaWqabeaacaaIYaaaaaWcbaGaeq4Wdm3aa0baaWqaaiaadMgaaeaacaaIYaaaaaaaaeaacaWGPbGaeyypa0JaaGymaaqaaiaad6gaa4GaeyyeIuoaaaGccaGGUaaaaa@6CB6@ If the
n random variables are all drawn from the same normal distribution with a mean of μ and a variance of
σ
2
,
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabeo8aZnaaCaaaleqabaGaaGOmaaaakiaacYcaaaa@394F@ then the pdf simplifies to
f
(
x
1
,
x
2
,
…
,
x
n
)
=
1
(
2
π
σ
2
)
n
/
2
e
−
1
2
σ
2
∑
i
=
1
n
(
x
i
−
μ
)
2
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAgadaqadaqaaiaadIhadaWgaaWcbaGaaGymaaqabaGccaGGSaGaamiEamaaBaaaleaacaaIYaaabeaakiaacYcacqWIMaYscaGGSaGaamiEamaaBaaaleaacaWGUbaabeaaaOGaayjkaiaawMcaaiabg2da9maalaaabaGaaGymaaqaamaabmaabaGaaGOmaiabec8aWjabeo8aZnaaCaaaleqabaGaaGOmaaaaaOGaayjkaiaawMcaamaaCaaaleqabaGaamOBaiaac+cacaaIYaaaaaaakiaadwgadaahaaWcbeqaaiabgkHiTmaalaaabaGaaGymaaqaaiaaikdacqaHdpWCdaahaaadbeqaaiaaikdaaaaaaSWaaabCaeaadaqadaqaaiaadIhadaWgaaadbaGaamyAaaqabaWccqGHsislcqaH8oqBaiaawIcacaGLPaaadaahaaadbeqaaiaaikdaaaaabaGaamyAaiabg2da9iaaigdaaeaacaWGUbaaoiabggHiLdaaaOGaaiOlaaaa@60C6@
Characteristics of an estimator of a population parameter θ
Finite estimators
Bias. The bias of an estimator is defined to be
B
(
θ
^
)
=
E
(
θ
^
)
−
θ
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadkeadaqadaqaaiqbeI7aXzaajaaacaGLOaGaayzkaaGaeyypa0JaamyramaabmaabaGafqiUdeNbaKaaaiaawIcacaGLPaaacqGHsislcqaH4oqCcaGGUaaaaa@4273@ An estimator is unbiased if and only if
B
(
θ
^
)
=
0.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadkeadaqadaqaaiqbeI7aXzaajaaacaGLOaGaayzkaaGaeyypa0JaaGimaiaac6caaaa@3C71@
Mean square error. The mean square error (MSE) of an estimator is defined to be
M
S
E
(
θ
^
)
=
E
[
(
θ
^
−
θ
)
2
]
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaad2eacaWGtbGaamyramaabmaabaGafqiUdeNbaKaaaiaawIcacaGLPaaacqGH9aqpcaWGfbWaamWaaeaadaqadaqaaiqbeI7aXzaajaGaeyOeI0IaeqiUdehacaGLOaGaayzkaaWaaWbaaSqabeaacaaIYaaaaaGccaGLBbGaayzxaaGaaiOlaaaa@4705@ It is relatively easy to show that
M
S
E
(
θ
^
)
=
V
(
θ
^
)
+
(
B
(
θ
^
)
)
2
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaad2eacaWGtbGaamyramaabmaabaGafqiUdeNbaKaaaiaawIcacaGLPaaacqGH9aqpcaWGwbWaaeWaaeaacuaH4oqCgaqcaaGaayjkaiaawMcaaiabgUcaRmaabmaabaGaamOqamaabmaabaGafqiUdeNbaKaaaiaawIcacaGLPaaaaiaawIcacaGLPaaadaahaaWcbeqaaiaaikdaaaGccaGGUaaaaa@4902@ Often a biased estimator with a smaller MSE may be preferred to an unbiased estimator with a relatively larger MSE.
Efficiency. An estimator
θ
^
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiqbeI7aXzaajaaaaa@37AF@ is relatively more efficient than
θ
˜
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiqbeI7aXzaaiaaaaa@37AE@ if and only if
V
(
θ
^
)
<
V
(
θ
˜
)
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAfadaqadaqaaiqbeI7aXzaajaaacaGLOaGaayzkaaGaeyipaWJaamOvamaabmaabaGafqiUdeNbaGaaaiaawIcacaGLPaaacaGGUaaaaa@3FF2@ Generally, we would prefer to use the most efficient estimator available (if it is unbiased).
Asymtoptic estimators
Plim.
x
n
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIhadaWgaaWcbaGaamOBaaqabaaaaa@3805@ converges to a constant,
c , if
lim
n
→
∞
Pr
(
|
x
n
−
c
|
>
ε
)
=
0
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiGacYgacaGGPbGaaiyBamaaBaaaleaacaWGUbGaeyOKH4QaeyOhIukabeaakiGaccfacaGGYbWaaeWaaeaadaabdaqaaiaadIhadaWgaaWcbaGaamOBaaqabaGccqGHsislcaWGJbaacaGLhWUaayjcSdGaeyOpa4JaeqyTdugacaGLOaGaayzkaaGaeyypa0JaaGimaaaa@4C21@ for any positive
ε
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabew7aLjaac6caaaa@3842@ We can write this relationship as
p
lim
x
n
=
c
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadchaciGGSbGaaiyAaiaac2gacaWG4bWaaSbaaSqaaiaad6gaaeqaaOGaeyypa0Jaam4yaiaac6caaaa@3E74@
Greene
offers this example of plim: Suppose
x
n
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIhadaWgaaWcbaGaamOBaaqabaaaaa@3805@ equals 0 with probability
1
−
(
1
n
)
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaaigdacqGHsisldaqadaqaamaalaaabaGaaGymaaqaaiaad6gaaaaacaGLOaGaayzkaaaaaa@3AD8@ and
n with probability
(
1
n
)
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaamaabmaabaWaaSaaaeaacaaIXaaabaGaamOBaaaaaiaawIcacaGLPaaacaGGUaaaaa@39E2@ As
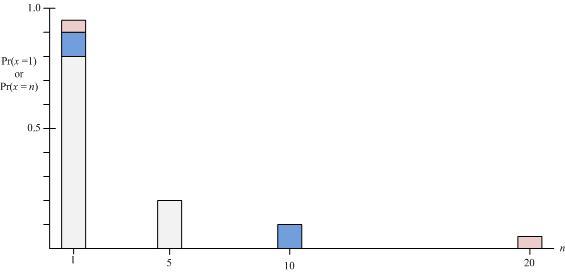
n increases, the second point becomes more remote from the first point. However, at the same time the probability of observing the second point becomes more and more unlikely. This effect is shown in Figure 5 where as
n increases the probability distribution concentrates more and more on 1.
Example of plim.
The probability x = 1 is the area of the gray box centered on 1 for n = 5; the gray area plus the blue area for n = 10; and the sum of the gray, blue, and red areas for n = 20; the probability x = n is the area of the box centered on n.
Consistency. The estimator
θ
^
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiqbeI7aXzaajaaaaa@37AF@ is a consistent estimator of
θ if and only if
p
lim
θ
^
=
θ
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadchaciGGSbGaaiyAaiaac2gacuaH4oqCgaqcaiabg2da9iabeI7aXjaac6caaaa@3EE2@
Asymmtotically unbiased. An estimator
θ
^
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiqbeI7aXzaajaaaaa@37AF@ is an asymtotically unbiased estimator of
θ if
lim
n
→
∞
E
[
θ
^
]
=
θ
.
MathType@MTEF@5@5@+=feaagyart1ev2aqatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLnhiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiGacYgacaGGPbGaaiyBamaaBaaaleaacaWGUbGaeyOKH4QaeyOhIukabeaakiaadweadaWadaqaaiqbeI7aXzaajaaacaGLBbGaayzxaaGaeyypa0JaeqiUdeNaaiOlaaaa@4530@
Source:
OpenStax, Econometrics for honors students. OpenStax CNX. Jul 20, 2010 Download for free at http://cnx.org/content/col11208/1.2
Google Play and the Google Play logo are trademarks of Google Inc.